Konu: Fonksiyon Kavramı ve Gösterimi

1. Fonksiyonlarla ilgili problemler çözer.

2. Fonksiyonların grafiklerini çizer.

3. Fonksiyonların grafiklerini yorumlar

4. Gerçek hayat durumlarından doğrusal fonksiyonlarla ifade edilebilenlerin grafik gösterimlerini yapar.

Konu: İki Fonksiyonun Bileşkesi ve Bir Fonksiyonun Tersi

1. Bire bir ve örten fonksiyonlar ile ilgili uygulamalar yapar.

2. Fonksiyonlarda bileşke işlemiyle ilgili işlemler yapar.

3. Verilen bir fonksiyonun tersini bulur.

10.2 FONKSİYONLAR

Fonksiyonların Kullanım Alanları

Fonksiyon 17. yüzyıldan beri matematiğin bir ana terimi olmuştur.Fizikte, mühendislikte, mimarlıkta ve bir çok alanda kullanılmaktadır

1- Araçlarda; yolculuk için, yoldaki tümseklere bağlı olarak yolcu koltuğunda aşağı yukarı hareket,fonksiyonla ifade edilir.

2- Yine araçlarda araç şekli ve Hızı bir fonksiyon olarak ifade edilir. Bu sayede pratik testler yapılmadan aracın aerodinamik şekline bağlı olarak, hızdaki değişime göre yakıt tüketimi hesabı yapılabilir.

3- Borsa grafikleri, paranın, dövizin, altının, petrolün değişim değerlerinin gösterildiği ve grafik gösteriminde işlemlerden yararlanılır.

Fonksiyon Tanımı

●A ve B boş olmayan iki küme olmak üzereA nın her bir elemanını B nin bir ve yalnız bir elemanına eşleyen ilişkiye (kurala) A dan B ye fonksiyon denir.

●A dan B ye tanımlı bir f fonksiyonuf :A→Bx→y=f(x): veya f :A→B, y=f(x) biçiminde gösterilir.

●A dan B ye tanımlı f kuralının fonksiyon olması için A daki her elemanın görüntüsü olmalı A daki her elemanın yalnız bir tane görüntüsü olmalı koşulları gerçeklenmelidir.

TANIM, DEĞER VE GÖRÜNTÜ KÜMESİ

● A dan B ye tanımlanan f fonksiyonu f: A → B şeklinde gösterilir. A kümesine tanım kümesi, B kümesine değer kümesi denir. A kümesinin elemanlarının, f fonksiyonuyla B kümesinde eşleştiği elemanlardan oluşan kümeye görüntü kümesi denir ve f(A) ile gösterilir. Görüntü kümesi değer kümesinin alt kümesidir.

●FONKSİYONUN SIRALI İKİLİLERLE GÖSTERİMİ

f fonksiyonu sıralı ikililer kullanılarak da gösterilebilir. Sıralı ikililerin ilk bileşeni tanım kümesinden, ikinci bileşeni değer kümesinden yazılır.

Örnek: K’dan L’ye tanımlı bir m fonksiyonu g = {(1, 10), (2, 15), (3, 10), (4, 20)} şeklinde verilsin. Bu fonksiyonun tanım ve görüntü kümesini bulalım.

Çözüm: Sıralı ikililerin ilk bileşenleri tanım kümesini, ikinci bileşenleri görüntü kümesini verir.g fonksiyonunun tanım kümesi, K = {1, 2, 3, 4}

g fonksiyonunun görüntü kümesi, g(K) = {10, 15, 20}

g fonksiyonunun değer kümesi olan L kümesini bulamayız. L kümesi görüntü kümesini kapsayan herhangi bir küme olabilir.

●Bu fonksiyonun hem tanım kümesi hem değer kümesi gerçek sayılar kümesi olduğu için bu fonksiyona “gerçek sayılardan gerçek sayılara tanımlı f fonksiyonu” demek yerine kısaca “gerçek sayılarda tanımlı f fonksiyonu” denilebilir.

Tanım kümesi ve değer kümesi aynı olan, A’dan A’ya tanımlı bir fonksiyona kısaca A’da tanımlı fonksiyon denilebilir.

ÖRNEK: f: R → R, f(x) = 10x + 9 fonksiyonu verilsin.Bu fonksiyonun hem tanım kümesi hem değer kümesi gerçek sayılar kümesi olduğu için bu fonksiyona “gerçek sayılardan gerçek sayılara tanımlı f fonksiyonu”demek yerine kısaca “gerçek sayılarda tanımlı f fonksiyonu” denilebilir.

ÖRNEK

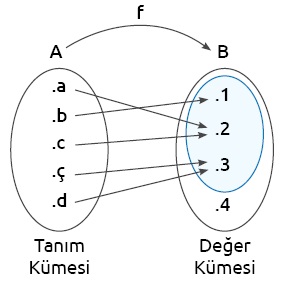
Aşağıda verilen f fonksiyonunun tanım, değer ve görüntü kümelerini bulalım. Fonksiyonu sıralı ikililerin kümesi şeklinde yazalım.

Çözüm: f fonksiyonunun tanım kümesi, A = {5, 7, 6, 3}

f fonksiyonunun değer kümesi, B = {2, 8, 6, 1}

f fonksiyonunun görüntü kümesi, f(A) = {8, 6, 1}

Sıralı ikililerle f fonksiyonu, f = {(5, 8), (7, 8), (6, 1), (3, 6)}

Fonksiyon Çeşitleri

Ürettikleri çıktılara göre, değer kümesi ve görüntü kümesinin birbiriyle ilişkisine göre çeşitli fonksiyon türleri vardır. Bu konuda fonksiyon çeşitleri olarak birim fonksiyon, sabit fonksiyon, doğrusal fonksiyon, eşit fonksiyon, tek fonksiyon, çift fonksiyon, parçalı fonksiyon, bire bir fonksiyon, örten fonksiyon ve içine fonksiyon yer almaktadır.

●BİRİM FONKSİYON

A boş kümeden farklı bir küme olmak üzere A’dan A’ya tanımlı, her elemanı kendine eşleyen fonksiyona birim fonksiyon (özdeşlik fonksiyon) denir ve I ile gösterilir.

Matematiksel olarak:A ≠∅I: A → A, I(x) = x

●SABİT FONKSİYON

f : A → B fonksiyonunda, A kümesinin bütün elemanları B kümesinin yalnız bir elemanı ile eşleniyorsa f fonksiyonuna sabit fonksiyon denir.

Matematiksel olarak:A, B ≠∅ ve k ∈ Bf: A → B, ∀x ∈ A için f(x) = k

●İÇİNE FONKSİYON

Bir fonksiyonun değer kümesinde en az bir eleman açıkta kalıyorsa, diğer bir ifadeyle görüntü kümesi ile değer kümesi eşit değilse bu fonksiyona içine fonksiyon denir.

Matematiksel olarak:A, B ≠∅ ve f: A → B olmak üzere,f(A) ≠ B ise f fonksiyonu içinedir.

●ÖRTEN FONKSİYON

Bir fonksiyonun değer kümesindeki her bir elemana karşılık tanım kümesinde en az bir eleman varsa, diğer bir ifadeyle görüntü kümesi ile değer kümesi eşit ise bu fonksiyona örten fonksiyon denir.

Matematiksel olarak:A, B ≠∅ ve f: A → B olmak üzere,f(A) = B ise f fonksiyonu örtendir

●BİRE BİR FONKSİYON

Bir fonksiyonun tanım kümesindeki her bir elemanın görüntüsü tanım kümesindeki diğer elemanların görüntülerinden farklı ise bu fonksiyona bire bir fonksiyon denir.

Matematiksel olarak:A, B ≠∅ ve f: A → B olmak üzere,∀x1, x2 ∈ A ve x1 ≠ x2 içinf(x1) ≠ f(x2) oluyorsa f fonksiyonu bir bir fonksiyondur.

●DOĞRUSAL FONKSİYON

a, b ∈ R olmak üzere; f: R → R, f(x) = ax + b fonksiyonuna doğrusal fonksiyon denir. Doğrusal fonksiyonların grafikleri doğru belirtir.

●EŞİT FONKSİYONLAR

Tanım ve görüntü kümeleri birbiriyle aynı olan, tanım kümesindeki her bir elemanı için bu elemanların görüntüleri de aynı olan fonksiyonlara eşit fonksiyonlar denir.

Matematiksel olarak:A ≠∅ ve B ≠∅f: A → B ve g: A → B olmak üzere,∀x ∈ A için f(x) = g(x) ise f = g’dir.

●PARÇALI FONKSİYON

Tanım kümesinin ayrık alt kümelerinde farklı kurallarla belirlenen fonksiyonlara parçalı fonksiyon ya da parçalı tanımlı fonksiyon denir. Kritik noktası a olan parçalı bir f fonksiyonu şu şekilde tanımlanabilir;
f(x)= g(x) ,x < a

h(x) ,x ≥ a

●TEK VE ÇİFT FONKSİYONLAR

f: R → R olmak üzere ∀x ∈ R içinf(−x) = f(x) olan f fonksiyonuna çift fonksiyon,f(−x) = −f(x) olan f fonksiyonuna tek fonksiyon denir.

~ Çift fonksiyonların grafikleri y eksenine göre simetriktir.

~Tek fonksiyonların grafikleri ise orijine göre simetriktir.

●FONKSİYONLARDA TOPLAMA İŞLEMİ

A ∩ B ≠∅ olmak üzere f: A → R ve g: B → R fonksiyonlarının toplamı şu şekilde tanımlanır;(f+g): A ∩ B → R

(f+g)(x) = f(x) + g(x)

●FONKSİYONLARDA ÇIKARMA İŞLEMİ

A ∩ B ≠∅ olmak üzere f: A → R ve g: B → R fonksiyonlarının toplamı şu şekilde tanımlanır;(f−g): A ∩ B → R

(f−g)(x) = f(x) − g(x)

●FONKSİYONLARDA ÇARPMA İŞLEMİ

A ∩ B ≠∅ olmak üzere f: A → R ve g: B → R fonksiyonlarının toplamı şu şekilde tanımlanır;(f.g): A ∩ B → R

(f.g)(x) = f(x) . g(x)

●FONKSİYONLARDA BÖLME İŞLEMİ

A ∩ B ≠∅ olmak üzere f: A → R ve g: B → R fonksiyonlarının toplamı şu şekilde tanımlanır;(f/g): A ∩ B → R

(f/g)(x) = f(x)/g(x) (g(x) ≠ 0)

●FONKSİYON GRAFİKLERİ

f : A → B, y = f (x) fonksiyonunu sağlayan bütün (x, y) sıralı ikililerinin dik koordinat sisteminde gösterilmesiyle oluşan noktalar kümesine f fonksiyonunun grafiği denir. Bu grafik çizilirken yatay eksende fonksiyonun tanım kümesinin elemanları, dikey eksende ise fonksiyonun değer kümesinin elemanları gösterilir.Bir fonksiyonun grafiği çizilirken fonksiyonun türüne göre farklı adımlar izlenir.

●DOĞRUSAL FONKSİYONLARIN GRAFİKLERİ

f : R → R, f (x) = ax + b biçimindeki doğrusal fonksiyonların grafikleri koordinat sisteminde y = ax + b doğrusudur ve bu doğru şu adımlar takip ederek çizilebilir:

► Doğrunun çizilebilmesi için geçtiği noktalardan en az 2 tanesi bilinmelidir. Bunun için fonksiyonu sağlayan (x, y) sıralı ikilileri bulunmalıdır.

► y = ax + b denkleminde x’e bir sayı değeri verilerek bu x’e karşılık gelen y değeri bulunur. Böylelikle bir tane (x, y) noktası elde edilmiş olunur.

► Aynı işlem, x’e farklı bir sayı değeri verilerek tekrarlanırsa ikinci (x, y) noktası da bulunmuş olunur.(x’e değer verip y bulunabildiği gibi y’ye değer verip x de bulunabilir.)

► Elde edilen noktalar koordinat sisteminde işaretlenir ve düz bir çizgiyle birleştirilir. Sonuç olarak f (x) = ax + b doğrusal fonksiyonunun grafiği çizilmiş olur.

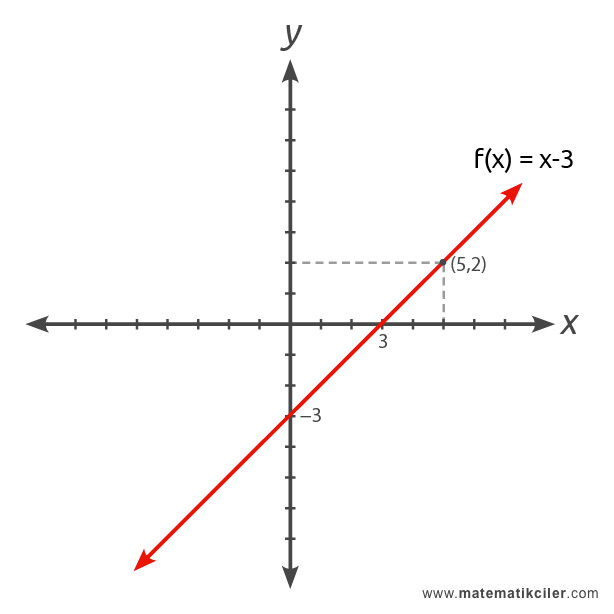
ÖRNEK: f : R → R olmak üzere f(x) = x − 3 fonksiyonunun grafiğini çizelim.

Doğrunun geçtiği noktalardan en az 2 tanesini buluruz. Bu noktaları bulmak için x’e ya da y’ye rastgele değer verebileceğimiz gibi x yerine “0” koyarak doğrunun y eksenini kestiği noktayı, y yerine “0” koyarak doğrunun x eksenini kestiği noktayı bulmamız hem çizim kolaylığı hem de genel kabule uyum açısından daha uygun olacaktır.

y = x − 3 denkleminde;
x yerine “0” koyarsak y için “−3” değerini,
x yerine “5” koyarsak y için “2” değerini,
y yerine “0” koyarsak x için “3” değerini buluruz.

Bulduğumuz bu üç noktayı koordinat sisteminde işaretleyip bu noktalardan geçen doğruyu çizeriz. Bu doğru f(x) = x−3 fonksiyonunun grafiğidir.

●DOĞRUSAL FONKSİYONLARDA KATSAYI GRAFİK İLİŞKİSİ

f (x) = ax + b fonksiyonunda a değerinin değişmesi fonksiyon grafiğinin eğiminin değişmesiyle sonuçlanır.

ÖRNEK: f(x) = 10x, g(x) = 3x, h(x) = x, t(x) = x/2 fonksiyonlarının grafiklerini inceleyelim

Grafikleri incelediğimizde bu fonksiyonların hepsinin y eksenini aynı noktada kestiğini ancak eğimlerinin (y’deki değişimin x’teki değişime oranlarının) farklı olduğunu görürüz.

Pozitif a değerinin (x’in katsayısının) artması grafiği y eksenine daha yakın bir hale getirir.

f (x) = ax + b fonksiyonunda b değerinin değişmesi fonksiyon grafiğinin yukarı ya da aşağı ötelenmesiyle sonuçlanır.

ÖRNEK: f(x) = x + 2, g(x) = x, h(x) = x − 1 fonksiyonlarının grafiklerini inceleyelim.

► g(x) = x fonksiyonu orijinden geçiyor.

► f(x) = x + 2 fonksiyonu y eksenini 2 noktasında kesiyor. Bu fonksiyon g(x) = x fonksiyonunun 2 birim yukarı ötelenmiş halidir.

► h(x) = x − 1 fonksiyonu y eksenini −1 noktasında kesiyor. Bu fonksiyon g(x) = x fonksiyonunun 1 birim aşağı ötelenmiş halidir.

PARÇALI FONKSİYONLARIN GRAFİKLERİ

Parçalı tanımlı fonksiyonların grafikleri çizilirken fonksiyon parçalarına ayrılır ve her bir parçanın grafiği ayrı ayrı çizilir. Daha sonra bu grafikler parçaların tanım kümesi aralıklarına göre alınıp birleştirilir.

ÖRNEK: p : R → R olmak üzere aşağıdaki şekilde tanımlanan parçalı fonksiyonun grafiğini çizelim.

p(x)=−2x ,x<−2

−x+2 ,−2 ≤ x < 3x

x−3 ,3 ≤ x

Fonksiyonun parçalarının ayrı ayrı grafiği çizilirse aşağıdaki gibi grafikler elde edilir.

Parçalı fonksiyonun kritik noktaları −2 ve 3 olduğu için bu kritik noktalara göre grafiklerin ilgili kısımlarını alacağız.

x’in −2’den küçük değerleri için kırmızı grafiği,
x’in [−2, 3) aralığındaki değerleri için yeşil grafiği,
x’in 3’e eşit ve 3’ten büyük değerleri için mavi grafiği alacağız.

Bu şekilde parçaları birleştirdiğimizde p(x) fonksiyonumuzun grafiği aşağıdaki gibi olur.

●Bileşke Fonksiyon

Örten bir fonksiyonun görüntü kümesinin başka bir fonksiyonun tanım kümesi olacak şekilde iki fonksiyonun tek bir fonksiyon haline gelerek oluşturduğu yeni fonksiyona bileşke fonksiyon denir.

Bir örnekle açıklarsak A kümesinden B kümesine tanımlı f fonksiyonu ve B kümesinden C kümesine tanımlı g fonksiyonu olsun. Biz direkt A kümesinden C kümesine tanımlı fonksiyon oluşturmak istediğimizde f ve g fonksiyonun bileşkesinden faydalanırız.

Bileşke fonksiyon (g∘f)(x)(g∘f)(x) şeklinde yazılır ve “g bileşke f” diye okunur.

f:A→B (örten)

g:B→C

g∘f : A→C, h = (g∘f)(x) = g[f(x)]

Bileşke fonksiyonlarda işlemler sağdan sola doğru yapılır. Bileşke fonksiyon iki veya daha fazla fonksiyondan oluşabilir. Her fonksiyon bir solundakinin içine yazılarak işlemler yapılabilir.

Aşağıda f ve g fonksiyonlarından oluşan bileşke fonksiyonu görsel olarak görebileceğimiz örneği inceleyelim.

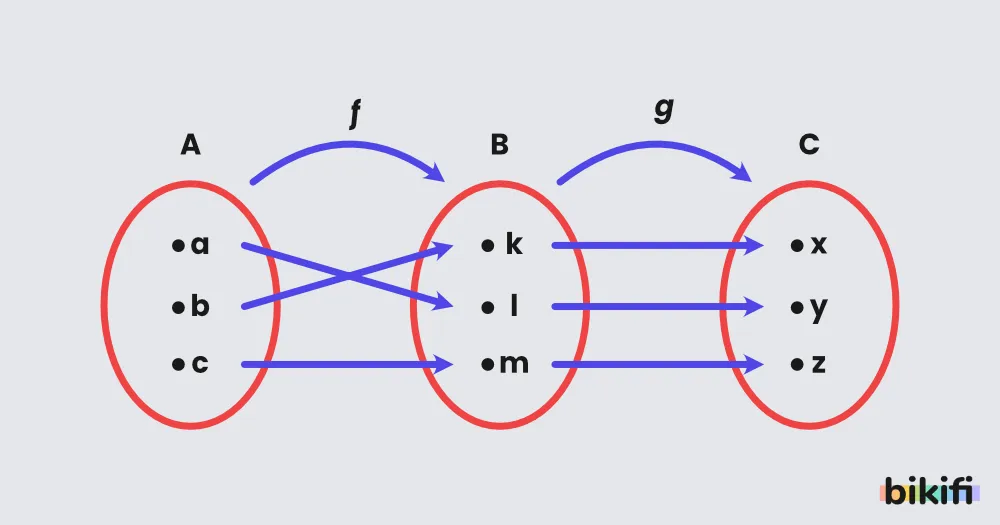
(g ∘ f)(a) = g[f(a)] = g(l) = y

(g∘f)(b) = g[f(b)] = g(k) = x

(g∘f)(c) = g[f(c)] = g(m) = z

● Bileşke Fonksiyonun Özellikleri

Özellik 1: Fonksiyonlarda bileşke işleminin değişme özelliği yoktur. Yani fonksiyonların yerlerini değiştiremeyiz. Sağdaki fonksiyonu soldakinin içine yazdığımız için bir yer değiştirme durumunda tam tersi şekilde birini diğerinin içine yazmak tamamen farklı bir sonuç getirecektir karşımıza.

g∘f ≠ f∘g

Özellik 2: Bir fonksiyonun birim fonksiyon (I(x)=xI(x)=x) ile bileşkesi kendisine eşittir. Birim fonksiyona ne verirsek aynısını aldığımız için sağ veya sol tarafta olması önemsizdir.

f∘I = I∘f = f

Özellik 3: Fonksiyonlarda bileşke işleminin birleşme özelliği vardır. Yani bileşke işlemlerini aralarındaki sıra bozulmadığı sürece istenilen yerden başlayarak yapabiliriz.

f∘g∘h=(f∘g)∘h=f∘(g∘h)

● BİR FONKSİYONUN TERSİ
f : A → B ye bire bir ve örten bir fonksiyon olmak üzere, B den
A ya tanımlanan fonksiyona f fonksiyonunun tersi denir.

f–¹ : B → A şeklinde gösterilir.

f(x) = y ise f–¹(y) = x tir.

Ters Fonksiyonla İlgili Özellikler

1. Bir fonksiyonun tersinin tersi kendisine eşittir.

2. f(x) = ax + b ise f–¹ (x) =x – b / a dır.

3. f : R — {–d / c} → R – {a / c} olmak üzere,

f(x) = ax + b / cx + d şeklinde bir fonksiyon ise tersi

f–¹ (x) = –dx + b / cx – a dır.

4. f : A → B ye bire bir ve örten bir fonksiyon olmak üzere,

f–¹: B → A fonksiyonunun grafiği, f(x) in grafiğinin y = x doğrusuna göre simetriğidir.