1.POLİNOM TANIMI
2.POLİNOMUN ÖZELLİKLERİ
2.1.Sabit polinom
2.2.Sıfır polinomu
3.POLİNOMUN EŞİTLİĞİ
4.POLİNOMLARDA DÖRT İŞLEM
4.1.Polinomlarda toplama çıkarma işlemi
4.2Polinomlarda çarpma işlemi
4.3.Polinomlarda bölme işlemi
POLİNOMUN GÜNLÜK HAYATTA KULLANILDIĞI YERLER
1.EKONOMİ
2.MÜHENDİSLİK
3.FİZİK
4.İSTATİSTİK
5.JEOLOJİ
6.TIP
7.BİLGİSAYAR BİLİMİ
8.ÇEVRE BİLİMLERİ
9.İNŞAAT
10.BİYOLOJİ
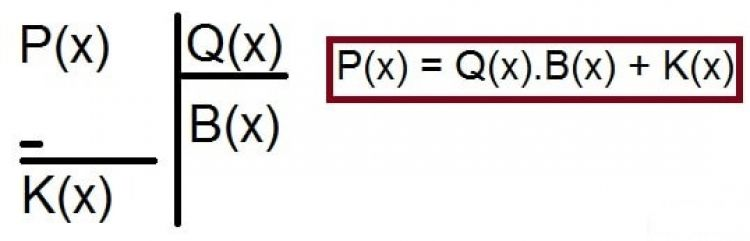
1.POLİNOM TANIMI
a0,a1,a2,a3 …, an ϵ R ve n ϵ N olmak üzere ;
P(x) = a0+a1.x+a2.x2+a3.x3+….+an.xn biçimindeki ifadelere x değişkenine göre
düzenlenmiş reel katsayılı polinom (çok terimli) denir.
an.xn terimindeki an sayısına terimin katsayısı, x’in kuvveti olan n sayısına terimin derecesi
olarak adlandırılır.
2.POLİNOMUN ÖZELLİKLERİ
2.1 Sabit Polinom
c ϵ R ve c≠0 ( c, 0 dan farklı bir reel sayı ) olmak üzere P(x) = c biçimindeki polinomlar
sabit polinom olarak adlandırılır. Sabit polinomun derecesi 0 dır.
2.2 Sıfır Polinomu
P(x) = 0 biçimindeki polinomu sıfır polinomu olarak adlandırılır. Sıfır polinomunun
derecesi tanımsızdır.
3.POLİNOMUN EŞİTLİĞİ
Aynı dereceli terimlerinin katsayıları eşit olan polinomlar eşittir.
4. POLİNOMLARDA DÖRT İŞLEM
4.1. Toplama İşlemi
İki polinom toplanırken; dereceleri aynı olan terimlerin katsayıları kendi aralarında
toplanır, o terimin kat sayısı olarak yazılır.
- xn + b. xn = (a + b). xn
- xn + b.xn = (1+b) . xn
4.2. Çıkarma İşlemi
İki polinom çıkarılırken; dereceleri aynı olan terimlerin katsayıları kendi aralarında
çıkarılır, o terimin katsayısı olarak yazılır.
4.3. Çarpma İşlemi
İki polinomun çarpımı; birisinin her teriminin diğerinin her bir terimi ile ayrı ayrı
çarpımlarından elde edilen terimlerin toplamına eşittir.- axn . bxm = a.b.xm+n
- xn . bxn = b.xn+m
4.4 Bölme İşlemi
P(x) : Bölünen
Q(x) : Bölen
B(x) : Bölüm
K(x) : Kalan
Olmak üzere bölme işleminde
- der [ P(x) ] ≥ der [ Q(x)]
- der [K(x) ] < der [ Q(x) ]
- P(x) = Q(x) . B(x) + K(x)
- der [ K(x) ] < der [B (x) ] ise Q (x ) ile B(x) in yer değiştirmesi kalanı
değiştirmez. - K (x) = 0 ise P(x) polinomu Q(x) polinomuna tm olarak bölünür. Bu
durumda P(x) in çarpanlarından biri Q(x) polinomudur.





Bir yanıt yazın