Mantık Nedir?

Mantık, akıl yürütme ve doğru düşünme kurallarını inceleyen bir disiplindir. Başlangıçta felsefe alanında bir konu olarak ele alınan mantık, zamanla matematiksel bir temele oturtmuş ve kendi başına bir bilim dalı haline geldi. Mantık, doğru ile yanlış arasındaki farkları belirler ve çıkarımların doğruluğunu test eder. Bu yüzden mantık, özellikle bilim, matematik, bilgisayar bilimi ve felsefe gibi alanlarda önemli bir yere sahiptir.

Mantık, belirli bir ifadenin doğru olup olmadığını belirlemenin yanı sıra, bir dizi önerme arasındaki ilişkileri de incelemeye olanak tanır. Örneğin, “Bütün insanlar ölümlüdür” gibi bir ifade, doğru ya da yanlış olarak değerlendirilebilir ve başka bir ifade ile ilişkilendirilir.

Mantığın Kullanım Alanları

1. Matematiksel ve Bilimsel Çalışmalar: Mantık, matematiksel teoremlerin ispatlanmasında, fizikte deney sonuçlarının analizinde ve çeşitli bilimsel araştırmaların sonucuna varılmasında önemli bir yer tutar. Herhangi bir bilimsel iddianın geçerli olabilmesi için mantıksal bir temele dayanması gerekmektedir.
2. Bilgisayar Bilimleri ve Yapay Zeka: Mantık, bilgisayar bilimlerinin temelini oluşturur. Yapay zeka, mantıksal çıkarımlar yaparak problemleri çözer. Özellikle veri tabanları, algoritmalar, programlama dilleri ve yapay zeka uygulamaları mantık kurallarına dayanır.
3. Hukuk: Hukuki argümanlar, mantıksal çıkarımlar ve doğruluklar üzerine inşa eder. Mahkemelerde, belirli önermelere dayalı argümanlar, yargıçlar ve avukatlar tarafından değerlendirir ve kararlar bu mantıksel çıkarımlar doğrultusunda verir.
4. Felsefe: Mantık, felsefi düşünme biçimlerinde önemli bir yer tutar. Felsefi argümanlar, mantıklı çıkarımlar yapılarak oluşturur. Aksi takdirde, felsefi düşünceler güvenilmez veya geçersiz sayar.
5. Günlük Yaşam: Mantık, günlük yaşamda karar verirken, tartışmalar yaparken veya sorunları çözmeye çalışırken de kullanır. İnsanlar, mantıklı düşünceler geliştirme ve çıkarımlar yapma yeteneği sayesinde karşılaştıkları problemleri çözebilirler.
6. Edebiyat ve Dilbilim: Mantık, dilbilimsel yapıların analizinde de kullanır. Dilin mantıksal yapısı, anlamların doğruluğu ve çelişkilerin analizi açısından dilbilimciler mantık kurallarını kullanır.

Önerme Nedir?

Önerme, doğru ya da yanlış olduğu kesin bir şekilde belirlenebilen bir ifadedir. Diğer bir deyişle, bir önermenin doğruluğu kanıtlanabilirsiniz. Ancak bir soru, emir ya da dilek cümlesi önerme olamaz, çünkü bu tür ifadelerin doğruluğu ya da yanlışlığı tartışmaya açıktır.

Örnekleri:

• Doğru bir önerme: “2’nin karesi 4’tür.”
• Yanlış bir önerme: “Bir ay 25 gündür.”
• Önerme olmayan bir ifade: “İyi geceler.”

Önerme, yalnızca doğru ya da yanlış olabilen bir yargıdır, ancak bir soru ya da emir gibi ifadeler bu kategorilere girmez.

Önerme Türleri

1. Basit Önerme: Bir basit önerme, tek bir doğruluğa sahip olan ve üzerinde herhangi bir işlem yapılmamış bir ifadedir. Yani, bir yargıyı ifade eden en temel önermedir. Örneğin:
   • “5 bir asal sayıdır.”
   • “10, bir çift sayıdır.”
2. Bileşik Önerme: İki veya daha fazla basit önermenin bir araya gelmesiyle oluşan önerme türüdür. Bileşik önerme, “ve”, “veya”, “ancak ve ancak” gibi bağlaçlarla oluşturur. Örneğin:
   • “5 bir asal sayıdır ve 7 bir asal sayıdır.”
     Burada iki basit önerme bağlanmış ve bileşik bir önerme oluşturulmuştur.
3. Denk Önermeler: İki önerme aynı doğruluk değerine sahipse, bu önermelere denk (eşdeğer) önermeler denir. Örneğin:
   • p: “Bir yıl 10 aydır.”
   • q: “Tam sayılar kümesi, rasyonel sayılar kümesini kapsar.”
     Burada p ve q her ikisi de yanlış olduğu için doğruluk değerleri eşittir.
4. Koşullu Önerme (İse Bağlacı): Bir koşullu önerme, “ise” bağlacı ile iki önermenin birbirine bağlanmasıyla oluşur. p => q şeklinde yazılıp ve “p ise q” olarak okur. Bu önerme, yalnızca p doğru ve q yanlış olduğunda yanlıştır. Diğer durumlarda doğrudur. Örneğin:
   • “Eğer yağmur yağarsa, zemin ıslanır.”
5. Açık Önerme: İçinde en az bir değişken barındıran ve bu değişkenlere belirli değerler verildiğinde doğruluğu ya da yanlışlığı belirlenebilen önermelere açık önerme denir. Bu tür önermelerin doğruluğunu anlamak için değişkenin yerine gerçek bir değer konulması gerekir.

Bir Önermenin Değili (Olumsuzluğu)

Bir önerme, belirli bir yargıyı ifade eder. Bir önermenin değili, o önerme ne söylüyorsa onun tam tersidir. Örneğin:

• Önerme: “Ankara, Türkiye’nin başkentidir.”
• Değili: “Ankara, Türkiye’nin başkenti değildir.”

Burada, değilli ifade (olumsuz önerme) verilen yargıyı olumsuzlamaktadır.

Doğruluk Tablosu

Mantıkta doğruluk tablosu, bir önerme veya bileşik önerme sisteminin doğru ya da yanlış olma durumlarını bir tabloda gösteren bir araçtır. Doğruluk tablosu, önerme mantığının temel bir aracıdır.

Örneğin, “veya” (/) bağlacının doğruluk tablosu şu şekilde olabilir:

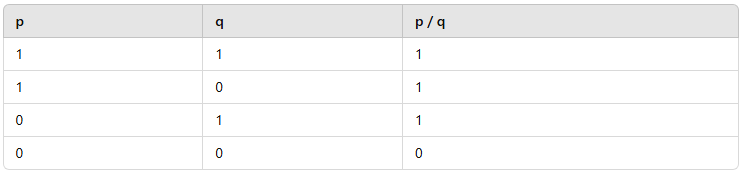
Burada, “veya” bağlacı kullanılarak yapılan bileşik önermenin doğruluk değeri belirtilmiştir. Yani, eğer p ya da q doğru ise, bileşik önerme de doğru olur.

Bağlaçların Özellikleri

Mantıkta kullanılan bağlaçlar, önermeleri birleştirirken bazı özellikler gösterir:

1. Tek Kuvvet Özelliği: Bir önerme kendisiyle “veya” bağlacı ile bağlandığında yine kendisiyle eşdeğerdir. Yani p / p = p.
2. Değişme Özelliği: Bağlaçlar, önermelerin sırasını değiştirdiğinizde bile aynı doğruluk değerini verir. Yani p / q = q / p.
3. Birleşme Özelliği: Bağlaçlar, parantezlerin değiştirilmesiyle de aynı sonucu verir. Örneğin, (p / q) / r = p / (q / r).
4. Dağılma Özelliği: Bağlaçlar, bir önerme üzerinde dağılabilirler. Yani p /\ (q / r) = (p /\ q) / (p /\ r).

İspat Yöntemleri

Mantık ve matematiksel çıkarımlar, bir önerme veya teoremin doğruluğunu kanıtlamak için çeşitli yöntemlere başvurur. Bu yöntemler, genellikle mantıklı bir sıra ile gerçekleştirir ve aşağıdaki başlıca yöntemler vardır.

1. Doğrudan İspat Yöntemi: Bir önerme doğrudan doğru olarak kabul edilir ve kanıtlanır. Bu yöntem, iddia edilen sonucu doğrudan ve açıkça kanıtlamayı hedefler.
2. Olmayana Ergi Yöntemi: Bir önerme, yanlışlık durumunu ele alarak kanıtlanır. Yani, önerme yanlış kabul edilir ve bu yanlışlık bir çelişki oluşturur.
3. Aksine Örnek Yöntemi: Bu yöntem, bir önerme doğruysa, onun tersini göstererek çelişki yaratmaya dayanır. Aksi örnek gösterilerek bir iddianın yanlış olduğu kanıtlanır.
4. Çelişki Yöntemi: Burada bir önerme kabul edilir, fakat çelişkiler ortaya çıkarsa bu durum önermenin yanlış olduğunu kanıtlar.

Niceleyiciler

• Evrensel Niceleyici (Her): Tüm elemanlar için doğru olan bir ifadeyi belirtir. “Her x, A’dır” gibi.
• Varlıksal Niceleyici (Bazı): Bir kümeye ait en az bir eleman için doğru olan bir ifadeyi belirtir. “Bazı x’ler A’dır” gibi.

Hazırlayan: Muhammed İlter Civelek 11/A 741