KÜMELERİN GERÇEK HAYATTA KULLANILDIĞI YERLER:

Evimizde, okulda, sokakta kısaca her yerde olayların birer küme halinde bulunduğunu düşünebiliriz. 

Örneğin;

Nesneleri sınıflandırmak için kullanırız.

Öğrencileri sınıflara ayırmak için kullanırız.

Eşyaları yerleştirmek için kullanırız. Mutfak dolaplarında yemek tabakları ile tencerelerin ayrı gözlerde bulunması kümelere örnek oluşturmaktadır.

Kütüphaneleri düzenlemek için kullanırız.

Hesaplamaları kolay yapabilmek için kullanırız.

Topluluk oluşturmak için kullanırız.

1. KÜMELER İLE İLGİLİ TEMEL KAVRAMLAR:

Alman matematikçi Georg Cantor (Corc Kantor) (1845-1918) 1878 yılında yayımladığı makalesinde kümeyi, “iyi tanımlanmış birbirinden farklı nesneler topluluğu’’
şeklinde tanımlamıştır. Bu tanımda bahsedilen “iyi tanımlama” ifadesi ortak özellikleri ile verilen bir kümedeki nesnelerin herkes tarafından aynı şekilde anlaşılma
sı, anlamına gelir. Örneğin Türk alfabesindeki ünlü harfler topluluğu iyi tanımlan
mış bir küme belirtir. Çünkü bu tanım herkesin aynı nesneleri düşünmesini sağlar.
Türk alfabesindeki bazı ünlü harfler topluluğu ifadesi ise herkesin aklına aynı harf
leri getirmeyeceğinden iyi tanımlanmış bir küme belirtmez.
Aşağıdaki topluluklar birer küme belirtir.
a) Kiremithane Mesleki ve Teknik Anadolu Lisesi Yeşilay Kulübü öğrencileri.
b) Asal sayılar.
c) Ardahan ilinin ilçeleri.
ç) 1 ile 2 arasındaki gerçek sayılar.

Bir kümeyi oluşturan her nesneye o kümenin bir elemanıdır, denir.
Kümeler A, B, C gibi büyük harflerle gösterilir.
4 ten büyük 10 dan küçük tam sayı ile ifade edilen kümeye A kümesi denilirse 5, 6,
7, 8, 9 sayılarının her biri bu kümenin bir elemanı olur.

KÜMELERİN FARKLI GÖSTERİMLERİ:

a) Liste Yöntemi: Kümelerin elemanları aralarına virgül konularak küme parantezi içinde yazılır.
b) Ortak Özellik Yöntemi: Kümelerin eleman sayıları çok ise
bu elemanlar ortak bir özelliğe göre yazılabilir.
c) Venn Şeması Yöntemi: Kümenin elemanları kapalı bir eğri
içinde “ ” nın yanına elemanın adı yazılarak gösterilir.

2. ALT KÜME:

Alt Kümenin Özellikleri:

1. Her küme kendisinin alt kümesidir.
   A ⊂ A
2. ∅ her kümenin alt kümesidir.
   ∅ ⊂ A
3. n elemanlı bir kümenin 2n tane alt kümesi, 2n – 1 tane öz
   alt kümesi vardır.
   Öz alt Küme:
   Kümenin kendisi hariç diğer alt kümelerine öz alt kümeleri
   denir.
   B kümesi A kümesinin alt kümesi ve A ≠ B ise B kümesine A
   kümesinin öz alt kümesi denir.
   B ⊂ A ile gösterilir.

Alt Küme Sayısı:
Boş küme her kümenin alt kümesidir.
A ={1, 2, 3} kümesinin elemanlarını kullanarak
• 3 elemanlı bir küme oluşturulursa {1, 2, 3},
• 2 elemanlı kümeler oluşturulursa {1, 2}, {1, 3}, {2, 3},
• 1 elemanlı kümeler oluşturulursa {1}, {2}, {3},
• 0 elemanlı bir küme oluşturulursa { },
olmak üzere toplam 8 tane alt küme oluşur

3. EŞİT KÜME:

Elemanları aynı olan kümelere eşit küme denir. A ve B kümelerinin eşitliği
A =B ile gösterilir.
A ve B iki eşit küme olmak üzere
• A kümesinin her elemanı B kümesinin de elemanı olduğu için

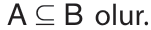
B kümesinin her elemanı A kümesinin de elemanı olduğu için

Bu durumda

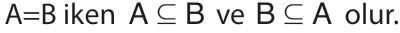
A ve B kümelerinin birbirinden farklı en az bir elemanı varsa A ile B eşit olmayan
kümelerdir denir ve bu durum A ≠ B ile gösterilir.

4. KÜMELERDE BİRLEŞİM, KESİŞİM, FARK ve TÜMLEME
İŞLEMLERİ:

Karanlıkta mavi, kırmızı ve yeşil ışık yayan üç farklı ışık
kaynağı şekildeki gibi bir zemine tutulursa mavi ve yeşil
ışığın düştüğü zeminin mavi, kırmızı ve yeşil ışığın düş
tüğü zeminin sarı, kırmızı ve mavi ışığın düştüğü zemi
nin koyu pembe renge dönüştüğü gözlemlenir. Her üç
ışığın düştüğü zeminin ise beyaz olduğu görülür. Elde
edilen yeni renkler diğer renkteki ışıkların kesiştiği böl
gede oluşmuştur.

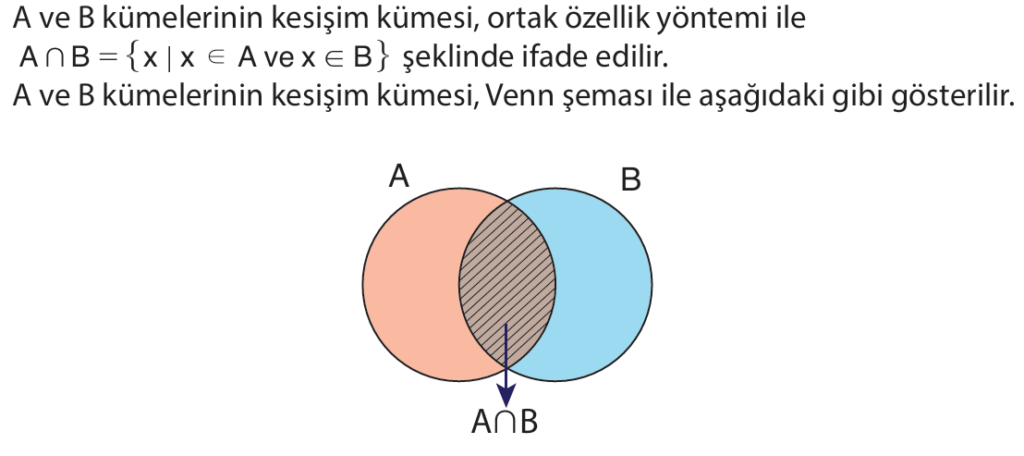
A ve B gibi iki kümenin tüm ortak elemanlarından oluşan kümeye A ve B kümelerinin kesişim kümesi adı verilir. Kesişim işlemi ” ” sembolü ile gösterilir

A ve B gibi iki kümenin bütün elemanlarından oluşan kümeye, A ve B kümelerinin birleşim kümesi adı verilir. Birleşim işlemi ” ” sembolü ile gösterilir

A ve B gibi iki kümenin bütün elemanlarından oluşan kümeye, A ve B kümelerinin birleşim kümesi adı verilir.

Kümelerde Fark İşlemi:

A ve B herhangi iki küme olmak üzere A kümesinde olup B kümesinde olmayan
tüm elemanların oluşturduğu kümeye A kümesinin B kümesinden farkı adı verilir. A − B veya A \ B ile gösterilir.

E evrensel kümesine ait bir A kümesi için A kümesinde bulunmayıp E kümesinde bulunan tüm elemanların oluşturduğu kümeye A kümesinin tümleyeni adı verilir ve
A` ile gösterilir. Ortak özellik yöntemiyle

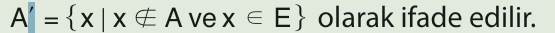
5. İKİ KÜMENİN KARTEZYEN ÇARPIMI:

Sıralı İkili
Her ikisi de boş kümeden farklı A ve B kümeleri için A kümesinden bir a elemanı, B kümesinden bir b elemanı alınarak elde edilen ve (a, b) şeklinde gösterilen ifadeye sıralı ikili adı verilir. Bu gösterimde “a” ya birinci bileşen, “b” ye ise ikinci bileşen adı verilir.
a ve b birbirinden farklı ise (a,b) ve (b,a) sıralı ikilileri de birbirinden farklıdır. Sıralı
ikili yazılımında bileşenlerin yazılış sırası önemlidir.
Sıralı İkililerin Eşitliği
(a, b) ve (c, d) sıralı ikilileri birbirine eşit ise bu durum (a, b) =(c, d) şeklinde gösterilir.
Bu eşitlikte a =c ve b =d olur.

Kartezyen Çarpım Kümesi
A ve B kümeleri boş kümeden farklı olmak üzere birinci bileşeni A kümesinden ikinci bileşeni B kümesinden alınarak oluşturulan tüm sıralı ikililerin kümesine A kartezyen çarpım B kümesi denir ve AxB ile gösterilir. AxB kümesinin ortak özellik yöntemi ile gösterimi

SORULAR: