Geometrik Şekiller Konu Anlatımı 10. Sınıf 1. tema olarak yeni maarif modelin ilk konusudur. Geometrik Şekiller Konu Anlatımı 9. sınıfta öğrendiğiniz benzerlik konusunu temel olarak alır. Geometrik Şekiller Konu Anlatımı yazımız ;
1.1. Dik üçgende trigonometrik oranlar ve trigonometrik özdeşlikler
1.2. Üçgende Yardımcı Elemanlar ve Bunlar Arasındaki İlişkiler
1.3. Üçgenin alanı
1.4. Sinüs ve kosinüs teoremleri
alt konu başlıklarından oluşmaktadır.
Bu temada sizlerden,
- dik üçgende trigonometrik oranlara (sinüs, kosinüs, tanjant, kotanjant) ve özdeşliklere ilişkin çıkarım yapabilmeniz,
- üçgenin yardımcı elemanlarının özellikleri ile ilgili çıkarım yapabilmeniz,
- üçgenin bir kenarı ve o kenara ait yüksekliğinin değişimine bağlı olarak alanının çıkarım yapabilmeniz.
- sinüs ve kosinüs teoremlerini doğrulayabilme veya ispatlayabilmeniz
- beklenmektedir.
1.1 Dik üçgende trigonometrik oranlar ve trigonometrik özdeşlikler
Matematikteki en önemli teoremlerden biri olan Pisagor Teoremi, Eski Mısır’da arazi ölçümlerinde sıklıkla kullanılmıştır. Günümüzde de uzunlukları ölçmede ve dik açıları oluşturmada birçok meslek grubu Pisagor Teoremi’nden yararlanmaktadır.
Trigonometri, haritacılardan grafik tasarımcılara, deprem bilimcilerden astronomiyle ilgilenenlere kadar birçok disiplinde kullanılmaktadır.
Pisagor Teoremi
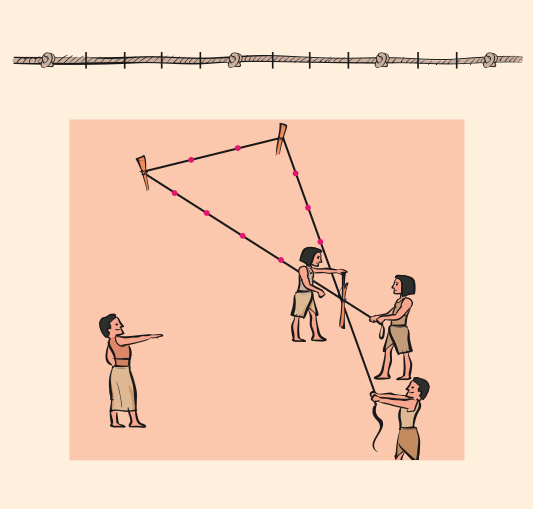
M.Ö. 570 ile M.Ö. 495 yılları arasında yaşadığı bilinen Pisagor’un ortaya attığı teorem geçmişte tarım alanlarının paylaşılması, arazi sınırlarının belirlenmesi gibi konularda kullanılmıştır. Ancak bu teoremin ve karşıtının Pisagor’dançok daha önceleri de kullanıldığı bilinmektedir. Örneğin eski Mısırlılar bir ipi 12 eş parçaya ayırarak 3, 4 ve 5 birim uzunluktaki iplerle dik açı elde etmişlerdir.

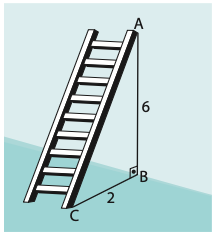
Şekildeki gibi duvara dayalı duran merdivenin A ucunun yerden yüksekliği 6 m, C ucunun duvara uzaklığı 2 m olduğuna göre merdivenin uzunluğunu bulalım.



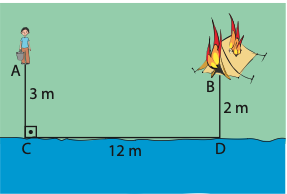
Yandaki şekilde kıyıdan 3 m uzaklıktaki A noktasında bulunan bir kişi, kıyıdan 2 m uzaklıkta B noktasındaki yanmakta olan çadırı söndürmek istiyor. Bunun için önce denize gidip elindeki kovayı su ile doldurması gerekiyor.
|CD| = 12 m olduğuna göre bu kişi çadırı söndürmek için en az kaç metre yol gitmelidir?
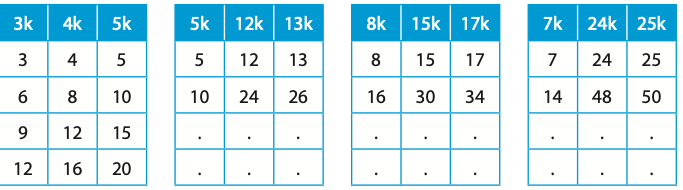
Aşağıda kenar uzunlukları tamsayı olan bazı dik üçgenler verilmiştir.
k pozitif bir reel sayı olmak üzere, kenar uzunlukları aşağıdaki gibi verilen üçgenler dik üçgenlerdir.
Dik Üçgende Dar Açıların Trigonometrik Oranları
Günümüzde astronomi, geometri, fizik, optik ve haritacılık gibi alanlarda sıklıkla kullanılan trigonometrinin ortaya çıkışı eski çağlara dayanmaktadır. Birçok bilim insanı Piri Reis’in Dünya haritasını hazırlarken trigonometriden yararlanmış olabileceğini dile getirmektedir.

Dik üçgenin açıları değiştirilmedikçe ilgili kenarlarının uzunlukları arasındaki oranlar da değişmemektedir. Dik üçgenin kenar uzunlukları arasında yer alan oranlara trigonometrik oranlar adı verilir. Bu bölümde sinüs, kosinüs, tanjant ve kotanjant isimleri ile bilinen trigonometrik oranlar incelenecektir.

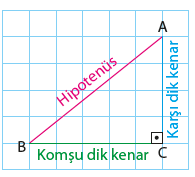
Verilen bir dik üçgende her zaman 90 derecenin karşısı HİPOTENUS sonra seçilen açıya göre komşu ve karşı dik kenar olarak isimlendirilir. yandaki üçgende seçilen açı B dir

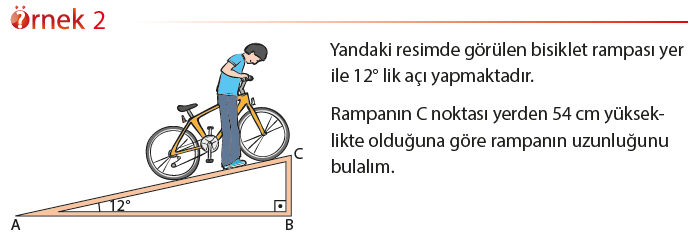


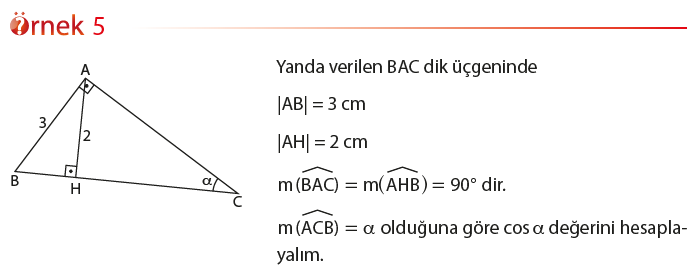

Bazı Açı Ölçülerinin (30° – 45° – 60°) Trigonometrik Oranları
30°, 45° ve 60° lik açı ölçülerinin trigonometrik oranlarını bulabilmek için bazı özel üçgenleri kullanacağız. Bu açı ölçülerinden 45° nin trigonometrik oranlarını ikizkenar dik üçgenden, 30° ve 60° nin trigonometrik oranlarını eşkenar üçgenden yararlanarak hesaplayacağız
45° – 45° – 90° Dik Üçgeni
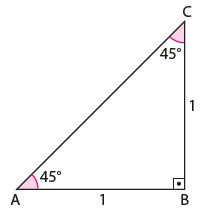
Yandaki ikizkenar dik üçgenin kenar uzunlukları arasındaki ilişkiyi inceleyerek 45° lik açının trigonometrik oranlarını bulalım. Dik kenar uzunlukları 1 birim olan ABC ikizkenar dik üçgenini ele alalım. Bu ikizkenar dik üçgenin hipotenüs uzunluğu
Pisagor Teoreminden bulunabilir.
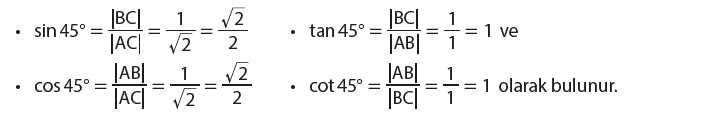
30° – 60° – 90° Dik Üçgeni
Üç kenarının uzunlukları birbirine eşit olan üçgene eşkenar üçgen denildiğini önceki
yıllarda öğrenmiştik. Bu bölümde eşkenar üçgenin bir kenarının uzunluğu ile bir kenarına ait yüksekliğinin uzunluğu arasındaki ilişkiyi ve 30° ile 60° nin trigonometrik oranlarını inceleyeceğiz.
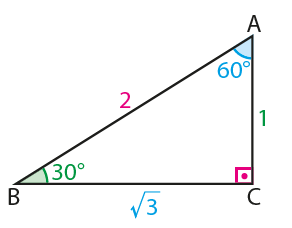
Dar açılarının ölçüleri 30° ve 60° olan bir dik üçgende kenar uzunlukları arasındaki ilişkiyi kullanarak bu açıların trigonometrik
oranları bulalım:
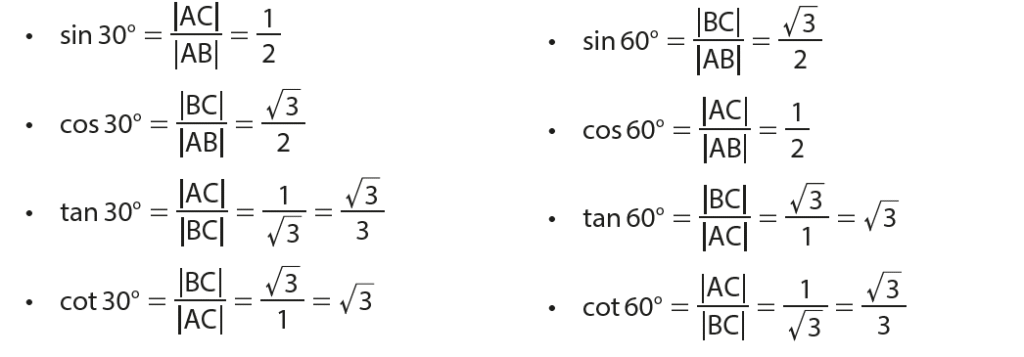
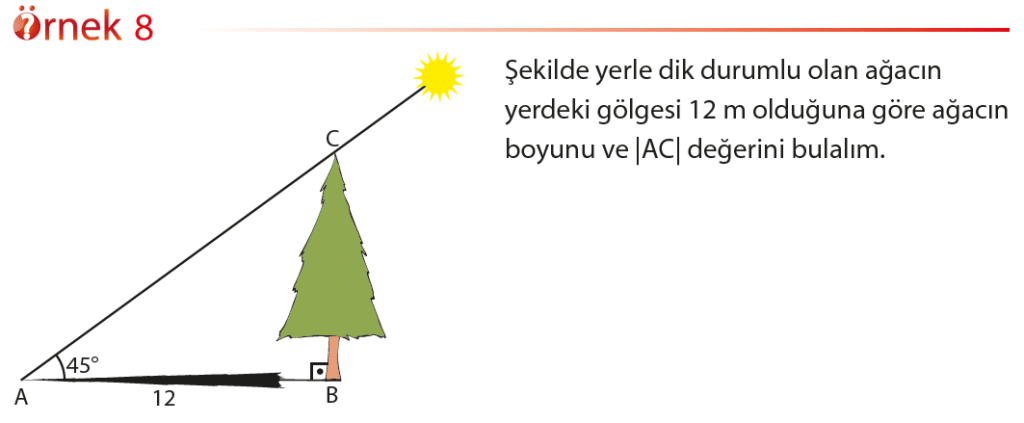

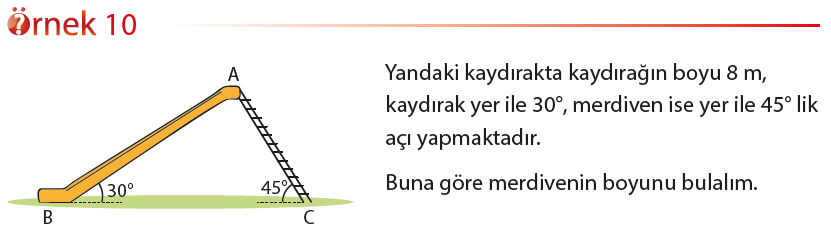

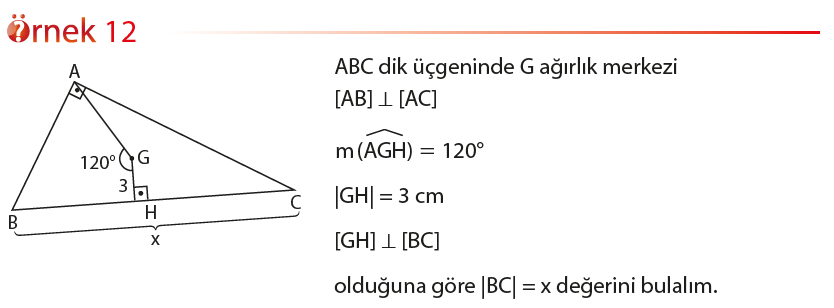
Yönlü Açı
Doğrusal hareket yapan bir cisim için yukarı-aşağı, sağa-sola gibi ifadeleri kullanırız. Peki çembersel hareket yapan bir cismin yönünü nasıl ifade edebiliriz? Örneğin, Dünya’mız kendi ekseninde ya da güneş etrafında hangi yönde dönmektedir?
Bir vidayı sıkarken ya da gevşetirken hangi yönde çevirirsiniz?

Evinizde kullandığınız şişe ve kavanoz kapakları, cıvata, vida ile muslukların hangi yöne açılıp kapandığını hatırlayınız . Ortak bir yönde açma ve kapama olup olmadığını gözlemleyiniz.
Saatin yelkovanının dönme yönü ile gözlem sonucunuzu ilişkilendirebilir misiniz? Dönme yönleri ile oluşan açının yönü arasındaki ilişkiyi ifade ediniz.

Saatin dönme yönüne negatif yön, saatin dönme yönünün tersine yöne
pozitif yön denir.

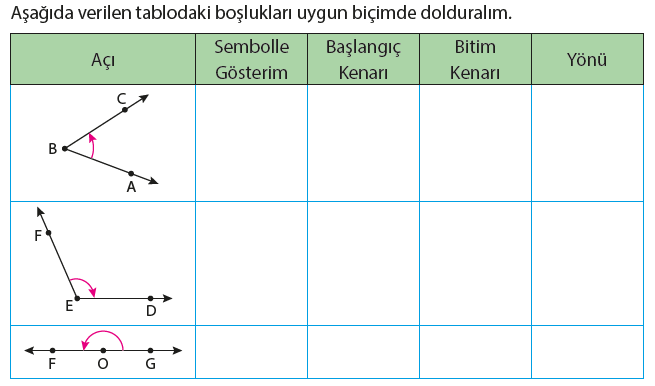
Yön kavramını açı kavramı ile de ilişkilendirebiliriz. Bir açının iki kenarı olduğuna
göre kenarlardan birini başlangıç, diğerini bitim kenarı olarak alalım.

Soldaki açı, başlangıç kenarı [OA, bitim kenarı [OB ye saat yönünün tersinde yani
pozitif yönde hareket ettiğinden pozitif yönlü açı olarak adlandırılır.
Sağdaki açı ise bu hareketi saat yönünde yani negatif yönde yaptığı için negatif
yönlü açı olarak adlandırılır.
Birim Çember
Önceki yıllarda dik koordinat sistemini ve koordinat sistemindeki noktaların gösterimlerini öğrenmiştiniz. Bir önceki bölümde ise dar açıların trigonometrik oranlarını bir dik üçgenin kenar uzunluklarından yararlanarak tanımlamıştık. Bu kısımda dar açılar için tanımladığımız trigonometrik oranları dik koordinat sistemi yardımıyla dik ve geniş açılar için de tanımlayacağız.
Merkezi orijin ve yarıçapı “1” birim olan çembere birim çember denir. Açıların trigonometrik oranlarını birim çember yardımıyla da bulabiliriz.
Dik koordinat düzleminin I. bölgesinde ve birim çember üzerinde bir A(x, y) noktasını ele alalım.
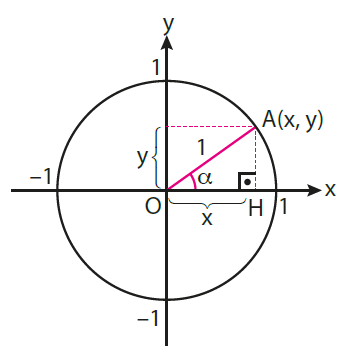
A noktasını orijine birleştiren doğru parçasını çizerek bu doğru parçasının eğim açısını a olarak isimlendirelim.
Yandaki şekilde oluşan AOH dik üçgeninde,
A noktasının koordinatları A(cos a, sin a)
şeklinde yazılabilir.
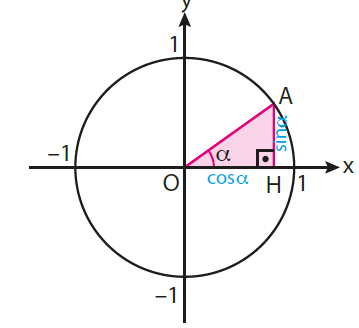
Başka bir ifadeyle A noktasının apsisi a nın kosinüs değerine, ordinatı a açısının sinüs değerine eşittir.
1.2. Üçgende Yardımcı Elemanlar ve Bunlar Arasındaki İlişkiler
Açıortay
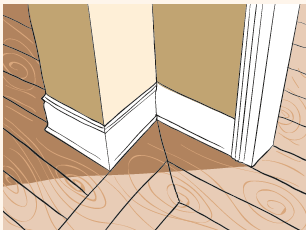
Oda duvarlarının zeminle birleştiği yerlerde kenar pervazları süpürgelik) bulunur. Marangozlar, kenar pervazlarını duvarların köşelerine yerleştirirken öncelikle duvarın köşe açısını belirlemek zorundadır. Bunun nedeni köşelerde süpürgeliklerin tam olarak birleşmesidir. Açı belirlendikten sonra her bir pervaz uçlarından belirlenen açının yarısı ölçüsünde kesilir. Böylece pervazlar duvarın köşelerinde tam olarak birleşir. Marangozlar aslında duvarın köşesinde oluşan açının açıortayını oluşturmaktadırlar.
Aşağıdaki çizim çalışmasında pergel-cetvel kullanılarak verilen bir açının açıortayının
nasıl çizilebileceği açıklanmıştır.

Yukarıdaki geometrik çizim çalışması sonucunda pergel ve cetvel kullanarak A nın
açıortayını çizdiniz. Şimdi de çizmiş olduğunuz [AN nın niçin A nın açıortayı olduğunu inceleyelim:
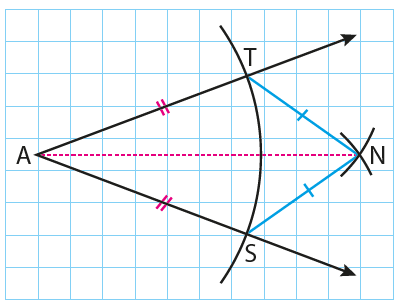
Bu şekilde T ve S noktalarından bir çizgi çizilirse oluşan alt ve üstteki iki üçgen benzer üçgen olur. K.K.K. benzerliğinden A ve N açıları eşit iki parçaya ayrılır.

Yukarıdaki teorem bir üçgenin açıortayı üzerinde alınan herhangi bir noktanın
açının kollarına eşit uzaklıkta olduğunu belirtmektedir. Bu teoremin karşıtı da
doğrudur. Bir açının iç bölgesinde alınan bir nokta açının kollarına eşit uzaklıkta
ise bu nokta açının açıortayı üzerindedir.


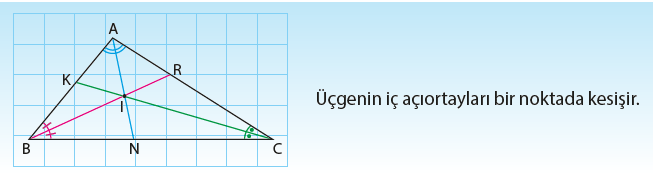
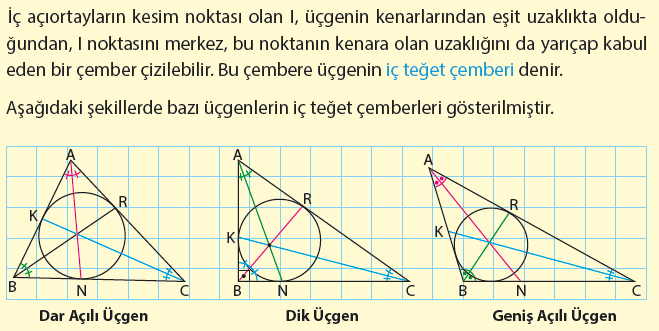
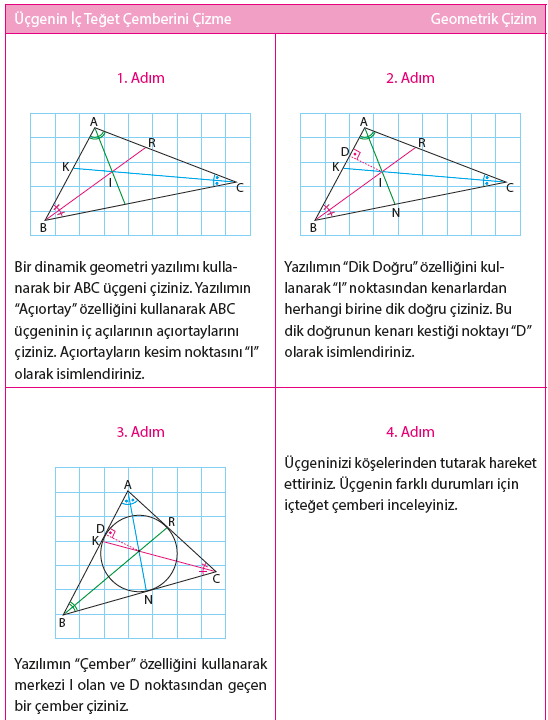
Üçgenin İç Açıortayları
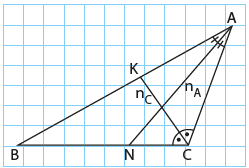
Bir üçgenin herhangi bir iç açısını eş iki parçaya bölen ışının, köşe ile karşı kenar arasında kalan parçasına, üçgenin o köşesine ait iç açıortayı denildiğini öğrenmiştik. Yandaki ABC üçgeninde [AN], A nı eş iki açıya böldüğünden, açıortaydır. Bir ABC üçgeninin “A” açısına ait açıortayın uzunluğu genellikle “nA”ile gösterilir







Üçgenin Dış Açıortayları
Bir üçgenin herhangi bir iç açıortayının karşı kenar üzerinde ayırdığı doğru parçalarının uzunluklarının üçgenin diğer kenar uzunlukları ile orantılı olduğunu öğrendik. Aşağıdaki teorem benzer bir ilişkinin dış açıortaylar için de geçerli olduğunu ifade etmektedir.




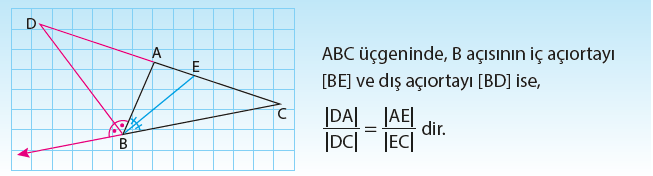
Hem dış açıortay hem de iç açıortay teoreminin birleşimidir. Ayrıca DBE açısı 90 derecedir.
Üçgende Kenarortay

Anadolu’nun en eski camilerinden biri olan Sivas Ulu Camii, minaresinin eğikliği ile dikkat çekmektedir. Caminin minaresi kendi eksenine göre 25° eğik durumdadır. Her yıl eğilmeye devam eden minarenin yıkılmaması için yenileme çalışmaları yapılmaktadır. Minarenin eğilmesine karşın henüz yıkılmamasının nedeni ağırlık merkezidir. Binalarda ağırlık merkezinin en uygun noktada oluşturulması
binanın her türlü yük altında daha dayanıklı olmasını sağlamaktadır.
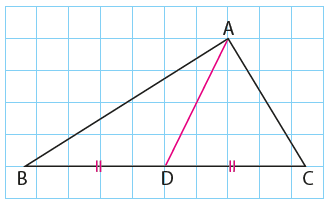
Bir üçgende, bir köşeyi karşısındaki kenarın orta noktasına birleştiren doğru parçasına, üçgenin o kenarına ait kenarortayı denildiğini öğrenmiştik.
Yandaki şekilde ABC üçgeninin BC kenarına ait AD kenarortayı çizilmiştir.
ABC üçgeninin a, b, c kenarlarına ait kenarortayların uzunlukları genellikle Va, Vb ve Vc ile gösterilir.






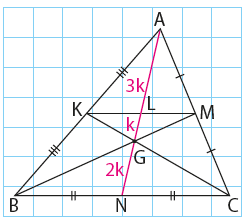
Üçgenin ağırlık merkezi ile
orta tabanın kenarortay
üzerinde ayırdığı uzunluklar
köşeden başlamak üzere 3,1
ve 2 sayılarıyla orantılıdır.
|AL| = 3k
|LG| = k
|GN| = 2k
Akılda kalması için 312 kuralı diye kodlayabiliriz.
Üçgenin Kenar Orta Dikme ve Yükseklikleri

Çekül, bir ipin ucuna küçük bir ağırlık bağlayarak düz, dikey bir çizginin elde edilmesi amacıyla oluşturulmuş bir araçtır. Marangozlar ve inşaat ustaları çekül kullanarak yaptıkları mobilya ya da
duvarların zemine dik ve düz bir yüzey oluşturup oluşturmadığını belirler.
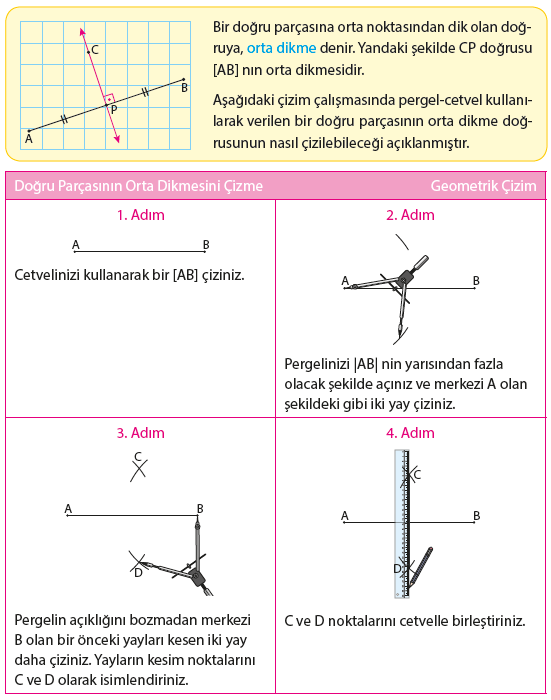
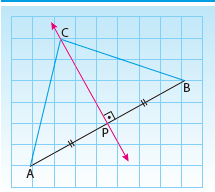
Bir doğru parçasının orta dikmesi üzerinde
alınan her nokta, doğru parçasının uç
noktalarına eşit uzaklıktadır.
Eğer CP, doğrusu [AB] nın orta dikmesi ise
|CA| = |CB| dir.

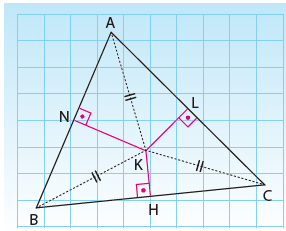
Bir üçgenin kenar orta dikmelerinin kesişim noktası üçgenin köşe noktalarından eşit uzaklıktadır.
Üçgenin kenar orta dikmelerinin kesim noktası üçgenin köşelerine eşit uzaklıkta
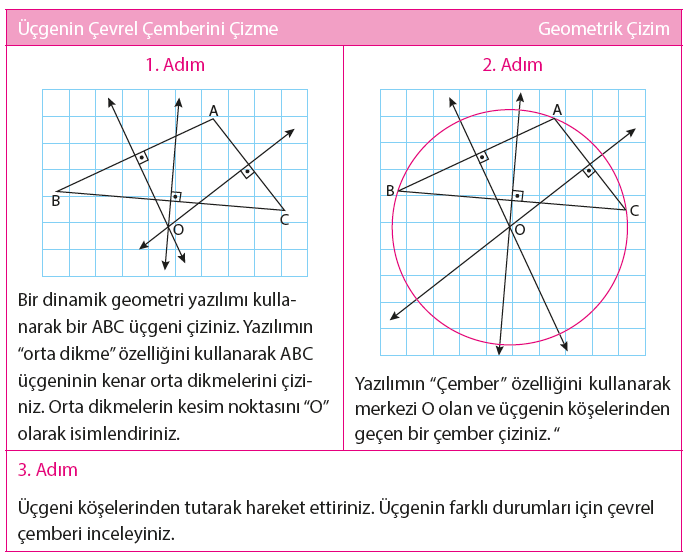
olduğundan, merkezi üçgenin kenar orta dikmelerinin kesim noktası olmak üzere
üçgenin köşe noktalarından bir çember geçer. Bu çembere üçgenin çevrel çemberi
ve bu çemberin merkezi olan kenar orta dikmelerinin kesim noktasına da üçgenin
çevrel çemberinin merkezi denir.
Üçgenin Yüksekliği
Bir üçgenin bir köşesinden karşı kenara veya karşı kenarın uzantısına indirilen dik
doğrunun, karşı kenarda kestiği nokta ile köşeyi birleştiren doğru parçasına, üçgenin
o kenarına ait yüksekliği denir.
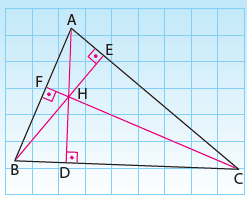
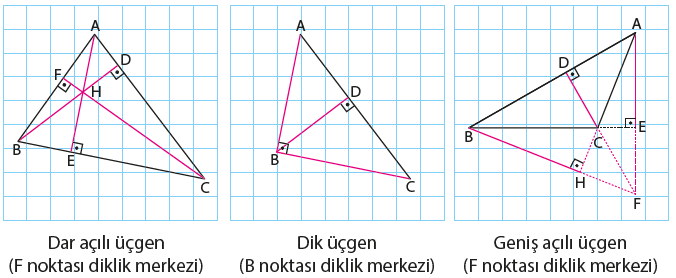
Bir üçgenin yükseklikleri aynı noktada kesişir. Bu noktaya üçgenin diklik merkezi denir.
Yandaki şekilde H diklik merkezidir.
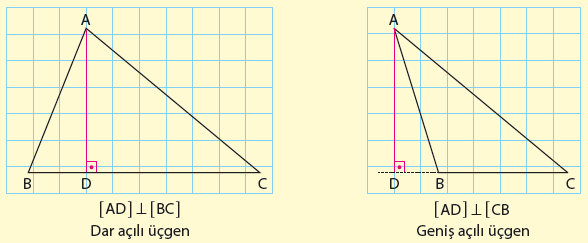
Yukarıdaki sonuca göre bir üçgenin yükseklikleri bir noktada kesişmektedir. Bu noktanın
yeri üçgenin açılarının türüne göre değişiklik göstermektedir. Aşağıdaki şekilde farklı üçgenlerin yüksekliklerinin kesim noktasının yeri gösterilmiştir.
1.3. Üçgenin alanı
İnşaat sektöründe ustalar, çatı, duvar ya da zemini kaplamadan önce ne kadar malzeme kullanacaklarını belirlemede geometrik şekillerin alanından yararlanırlar. Örneğin yandaki şekilde bir üçgenin alanını bularak tüm çatı için gerekli olan toplam cam miktarı belirlenebilir.

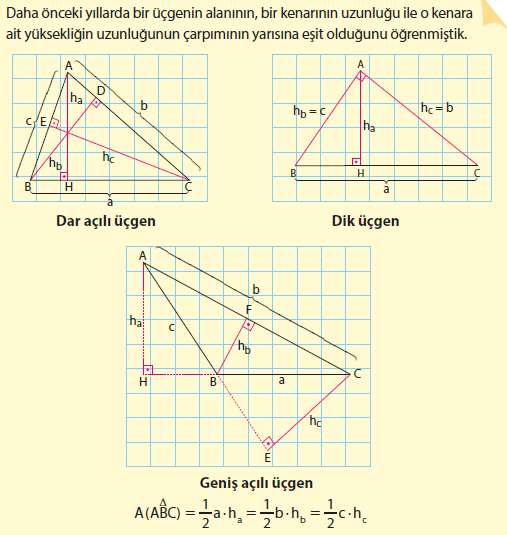
Üçgende alan hesaplaması bir çok yöntem ile olmaktadır. Yukarıdaki formül en çok kullanılan ve bilinen formüldür. Sırayla diğer formülleri inceleyelim.
Sinüs Alan Formülü


Heron Formülü

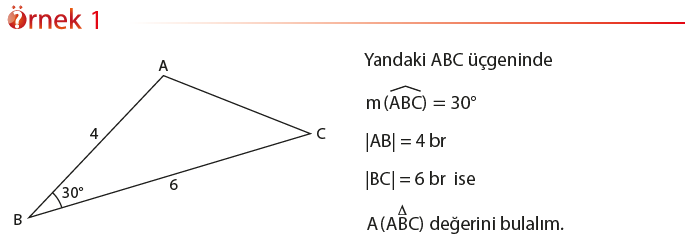
Kenar uzunlukları a = 5 br, b = 6 br ve c = 7 br olan ABC üçgeninin alanını ve b kenarına ait yüksekliğinin uzunluğunu bulalım.


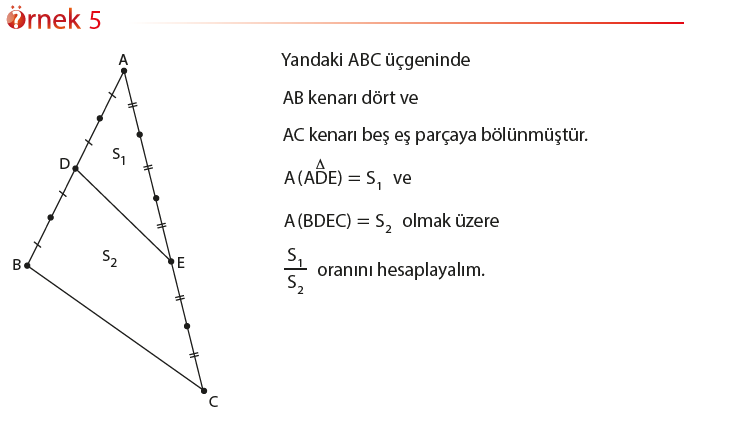
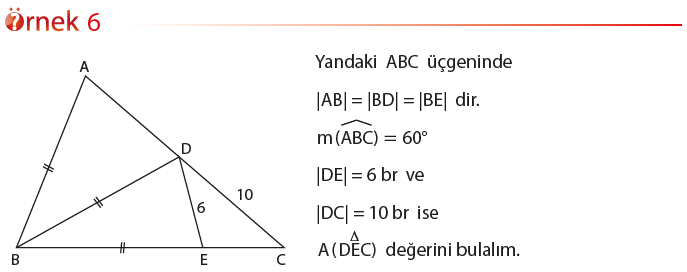
Eş Yüksekliğe veya Kenara Sahip Üçgenlerin Alanlarının Karşılaştırılması
- Birer kenarları eş olan üçgenlerin alanları oranı, eş olan kenarlara ait yükseklik uzunluklarının oranına eşittir.
- Yükseklikleri eş olan üçgenlerin alanları oranı, bu yüksekliklere ait kenar uzunluklarının oranına eşittir.
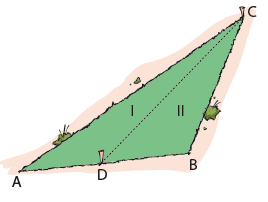
Üçgen şeklindeki tarlasını iki oğlu arasında eşit paylaştırmak isteyen Hasan Amca tarlanın bir kenarının ortasına bir kazık çakmıştır. Tarlanın bu kenarının karşısındaki köşeye de diğer bir kazık çakarak iki kazık arasına ip bağlamıştır. Oluşan iki parça tarlanın birinci kısmını büyük oğluna ikinci kısmını ise küçük oğluna vermiştir. Büyük oğlu kardeşinin kendisinden daha fazla tarladan pay
aldığını iddia ederek itiraz etmiştir. Hasan Amca’nın büyük oğlunun haklı olup olmadığını bulalım.

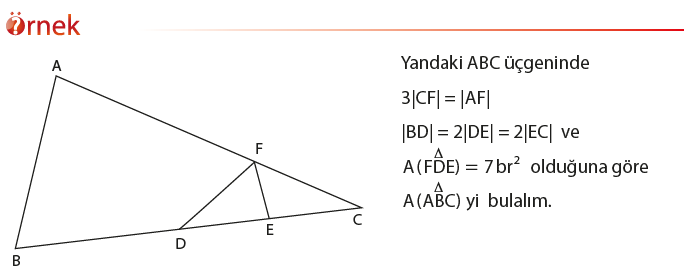

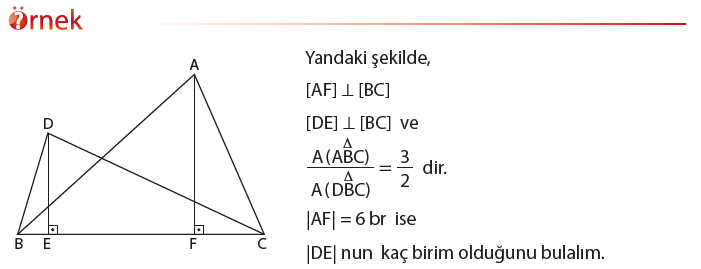
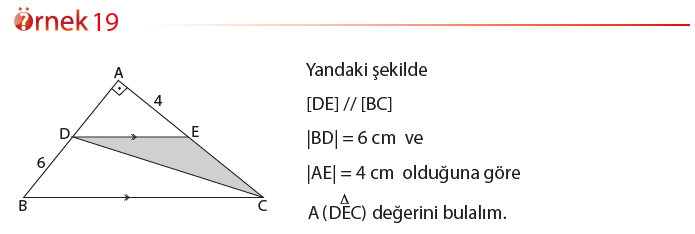
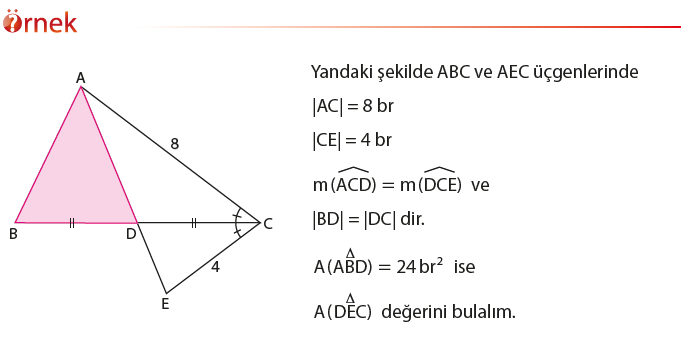
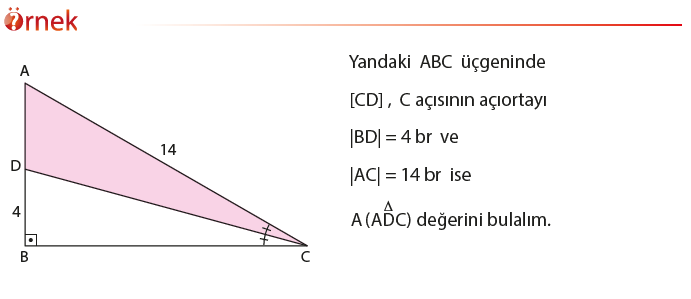
Bir üçgenin bir köşesinin, bu köşenin karşısındaki kenara paralel olan bir doğru üzerinde hareket ettirilmesi üçgenin alanını değiştirmez.
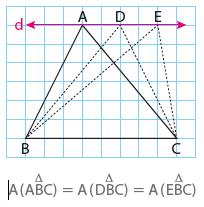
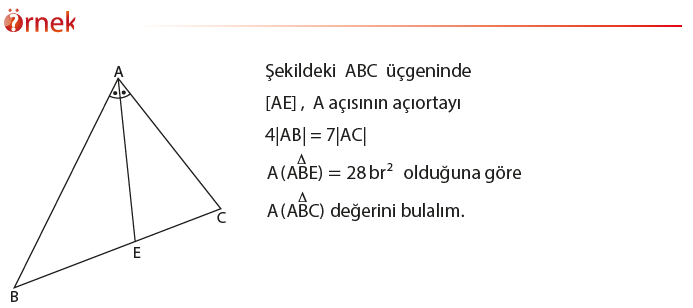
1.4. Sinüs ve Kosinüs teoremleri
Sinüs Teoremi
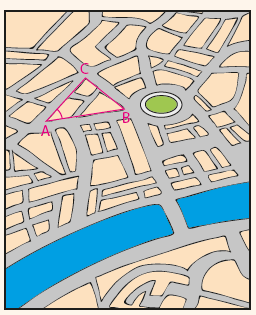
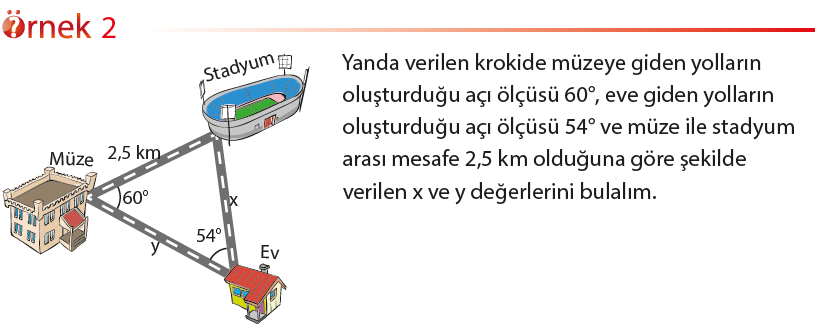
Bir harita veya kroki üzerinde belirli noktaların birbirlerine uzaklıkları ve bu noktaları birleştiren yolların oluşturduğu açı ölçülerinden bazılarının bilinmesi
durumunda bilinmeyen uzaklıkların bulunmasında Sinüs Teoremi kullanılabilir.
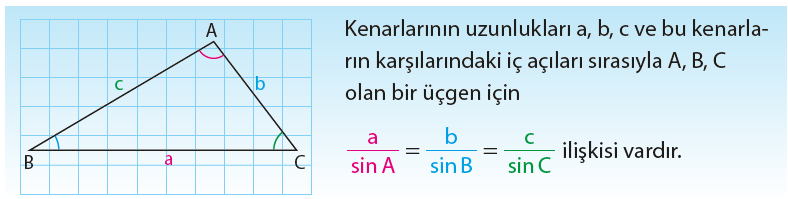
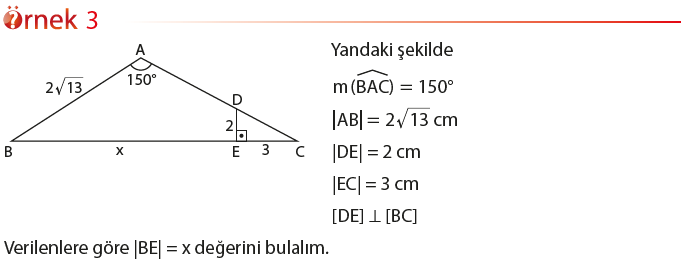
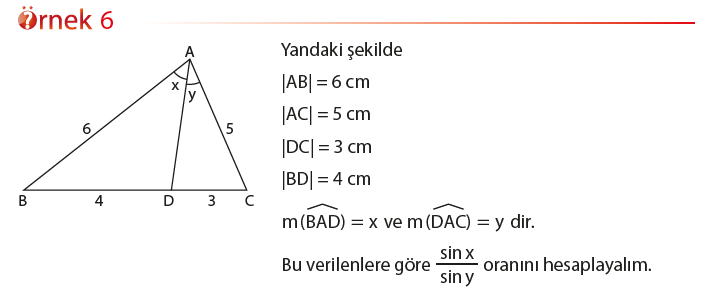
Bu bölümde bir üçgenin açı ölçüleri ve kenar uzunluklarından bazılarının verilmesi durumunda diğerlerini nasıl hesaplayacağımızı öğreneceğiz. Aşağıdaki teorem üçgenin açı ölçülerinin sinüs değerleri ile kenar uzunlukları arasında nasıl bir ilişki bulunduğunu ifade etmektedir. Bu teorem Sinüs Teoremi olarak bilinmektedir.



Kosinüs Teoremi
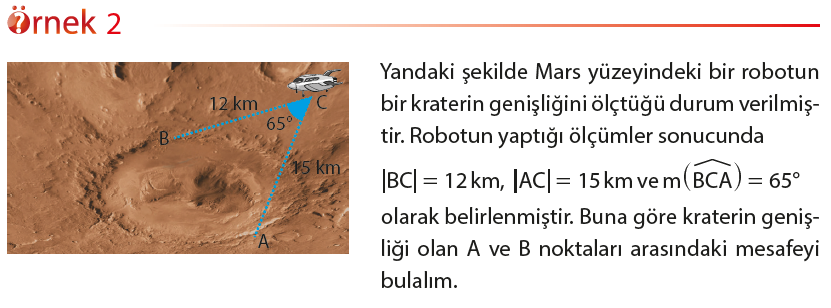
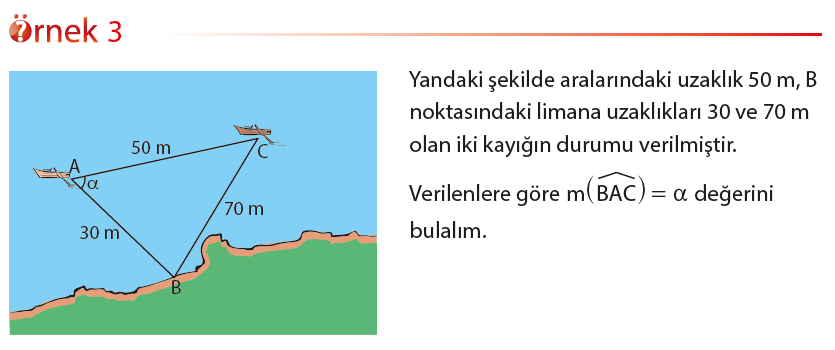
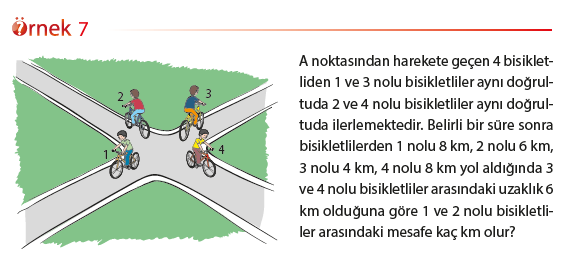
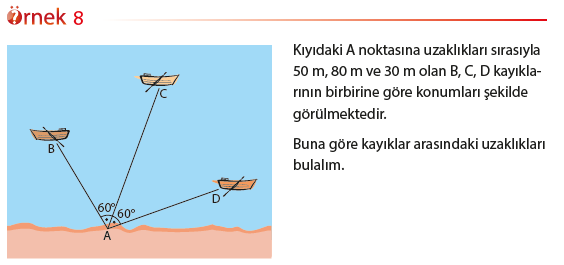
Mars yüzeyi üzerindeki kraterlerin genişliği hesaplanırken kosinüs teoreminden yararlanılır. Bu yöntemde, robotlar kraterin içine girmeden, kraterin genişliğini görecek noktaları belirleyerek bu noktaların referans noktasına uzaklıklarını bulup, referans açısını kullanarak kraterin genişliğini hesaplarlar.

Bu bölümde iki kenarının uzunlukları ve bu kenarların oluşturduğu açının ölçüsünün bilinmesi durumunda, bir üçgenin üçüncü kenar uzunluğunun nasıl hesaplanacağını öğreneceğiz. Aşağıdaki teorem, üçgenin iki kenar uzunluğu ve bu kenarların oluşturduğu açının ölçüsü ile üçüncü kenarının uzunluğu arasında nasıl bir ilişki olduğunu ifade etmektedir. Bu teorem kosinüs teoremi olarak ifade edilir.





Bir yanıt yazın