BİRİNCİ DERECEDEN DENKLEMLER VE EŞİTSİZLİKLER aklımıza gelebilecek her alanda kullanılıyor.

BİRİNCİ DERECEDEN DENKLEMLER KULLANIM ALANLARI:

Maliye ve Ekonomi

Bütçe hesaplamaları: Bir şirketin ya da bireyin gelir ve giderlerini dengelemeye yönelik denklemler oluşturulabilir. Örneğin, bir ürünün fiyatı ve üretim maliyetleri arasındaki ilişkiyi tanımlayan denklemler.

• Kredi ödemeleri: Banka kredisi alırken, kredi miktarı, faiz oranı ve ödeme planı arasındaki ilişki birinci dereceden denklemle ifade edilebilir.

Fizik:

• Hız, mesafe ve zaman ilişkisi: Hız, mesafe ve zaman arasındaki ilişki de doğrusal bir denklemle ifade edilebilir. Örneğin, bir aracın sabit hızla hareket ettiği durumda mesafe ve zaman arasındaki ilişki s=vts = vts=vt (mesafe = hız × zaman) şeklinde bir doğrusal denklemle ifade edilir.

İnşaat ve Mühendislik:

• Malzeme miktarları ve maliyet hesaplamaları: İnşaat sektöründe, malzeme miktarları ve maliyetler arasındaki ilişkiyi birinci dereceden denklemlerle hesaplamak mümkündür.
• Elektrik mühendisliği: Elektrik devrelerinde, akım, direnç ve voltaj arasındaki ilişkiyi tanımlayan Ohm Yasası V=IRV = IRV=IR doğrusal bir denklemle açıklanır.

Tarım ve Üretim:

• Verim ve maliyet hesaplamaları: Tarımda ürünlerin üretim maliyetlerinin hesaplanmasında, birinci dereceden denklemler kullanılır. Örneğin, bir çiftçinin birim başına malzeme ve iş gücü maliyetlerini hesaplamak için doğrusal modeller kurması gerekebili

BİRİNCİ DERECEDEN EŞİTSİZLİKLER KULLANIM ALANLARI:

Ekonomi ve Finans

• Bütçe kısıtlamaları: Bir işletmenin veya bireyin belirli bir bütçe ile harcama yapması gerektiğinde, eşitsizlikler kullanılarak bütçe sınırları belirlenir. Örneğin, bir şirketin aylık giderlerinin belirli bir tutarın altında kalması gerekebilir, bu da bir eşitsizlikle ifade edilir.
• Gelir dağılımı: Gelir eşitsizliklerini göstermek için eşitsizlikler kullanılır. Zenginlik ve yoksulluk arasındaki farkları analiz etmek veya sosyal eşitsizliği incelemek için de eşitsizlikler önemlidir.

Fizik ve Kimya

• Enerji ve güç sınırları: Fizikte, bir sistemin belirli bir enerji seviyesini geçmemesi gerektiği durumlar için eşitsizlikler kullanılır. Örneğin, bir motorun ısınma sınırının aşılmaması için belirli bir güç tüketimi eşitsizlikle ifade edilir.
• Kimyasal reaksiyonlar: Bir kimyasal reaksiyonun gerçekleşebilmesi için, belirli koşullar altında (örneğin sıcaklık, basınç, reaktant miktarı) eşitsizlikler kullanılarak hangi koşulların sağlanması gerektiği hesaplanabilir.

Sağlık ve Tıp

• İlaç dozajları ve hastalık yönetimi: Bir hastanın alması gereken ilaç miktarı, vücut ağırlığı ve sağlık durumu göz önüne alındığında, eşitsizlikler kullanılarak doğru dozaj hesaplanabilir. Örneğin, ilaç dozunun bir sınır değerin altında olması gerektiği durumu eşitsizlikle ifade edebiliriz.
• Ağırlık ve beslenme: Kilo yönetimi, beslenme diyetleri gibi sağlık alanlarında, tüketilen kalori miktarının belirli bir seviyenin altında kalması gerektiği durumlar için eşitsizlikler kullanılır.

Birinci Dereceden Denklemler

Derecesi (kuvveti) bir olan bilinmeyenlerden oluşan ve aşağıdaki şekilde ifade edilebilen denklemlere birinci dereceden denklem ya da lineer denklem denir.

a₁,a₂,…,a_n ∈ R

(a₁,a₂,…,a_n)≠(0,0,…,0) olmak üzere,

a₁x₁+a₂x₂+…+a_nx_n+b=0

---

ÖRNEK:

5x+15=0

3x−4y−17=0

−x+2y+3z+9=0

Bu denklemde x₁,x₂,…,x_n denklemin bilinmeyenleri, a₁,a₂,…,a_n ve b denklemin katsayılarıdır. b katsayısı aynı zamanda denklemin sabit terimidir.

Bir bilinmeyenli bir lineer denklemin çözümü x=c şeklinde tek bir değerdir ve sayı doğrusu üzerinde bir nokta olarak gösterilir.

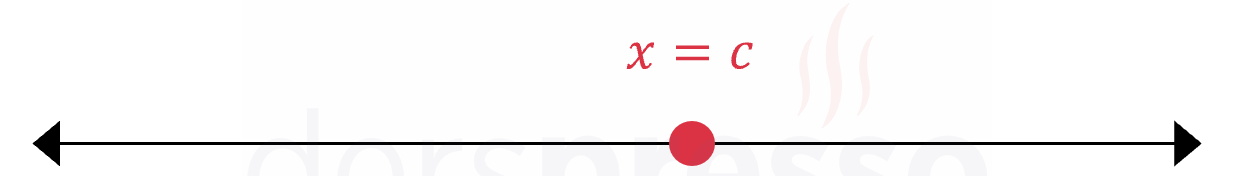
1. dereceden bir bilinmeyenli denklemlerin çözümü

İki bilinmeyenli bir lineer denklemin sonsuz sayıda çözümü vardır ve çözüm kümesi koordinat düzleminde bir doğruya karşılık gelir. Çözüm kümesindeki her bir çözüm bu doğru üzerinde koordinatları (x₁,x₂)=(c₁,c₂) sıralı ikilisi ile ifade edilen bir noktadır.

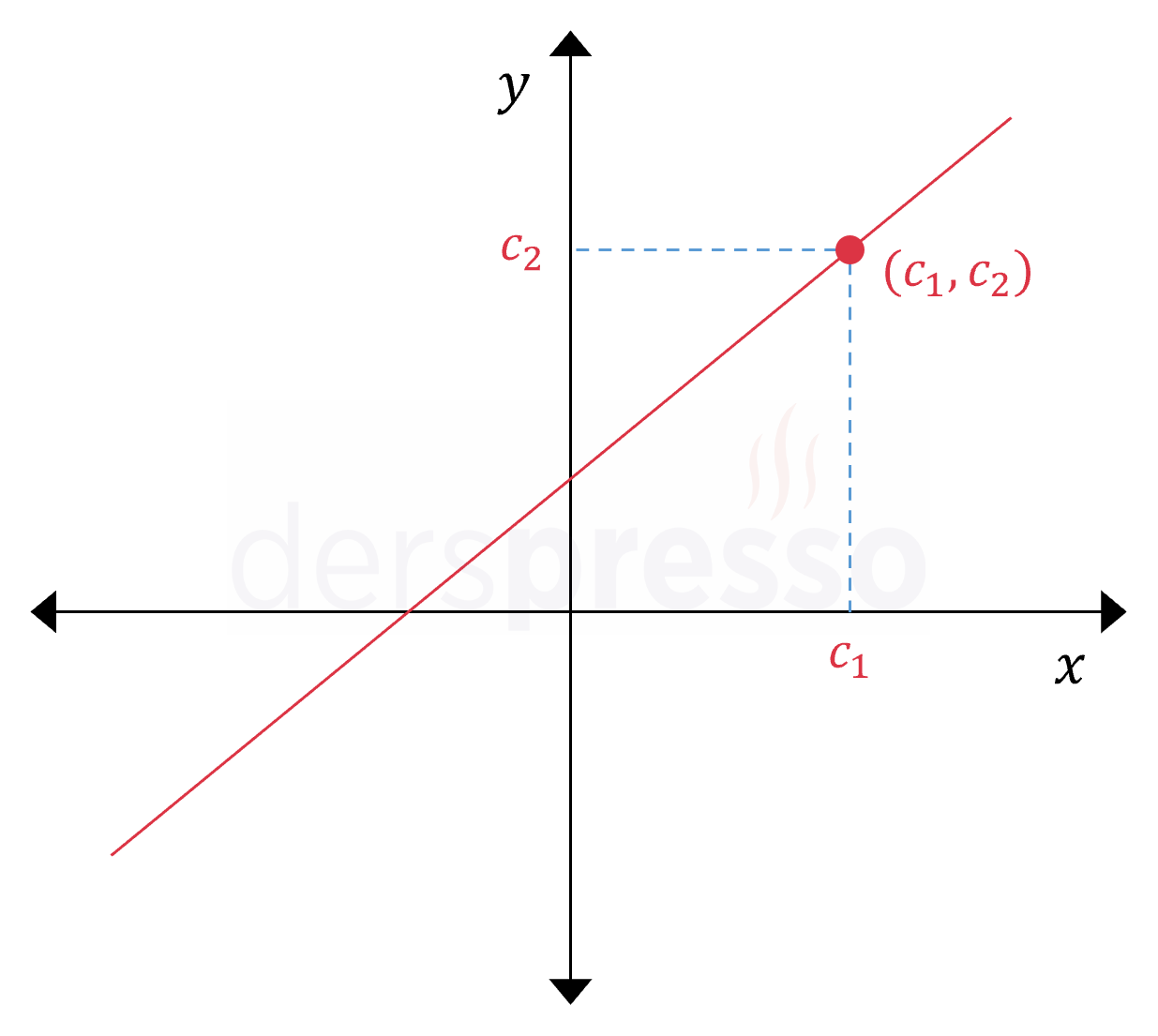
Birinci dereceden denklemlerin bir diğer adı olan “lineer” ifadesi de iki bilinmeyenli durumda denklemin çözüm kümesinin oluşturduğu doğrudan gelmektedir.

Üç bilinmeyenli bir lineer denklemin de sonsuz sayıda çözümü vardır ve çözüm kümesi koordinat sisteminde bir düzleme karşılık gelir. Çözüm kümesindeki her bir çözüm bu düzlem üzerinde koordinatları (x₁,x₂,x₃)=(c₁,c₂,c₃) sıralı üçlüsü ile ifade edilen bir noktadır.

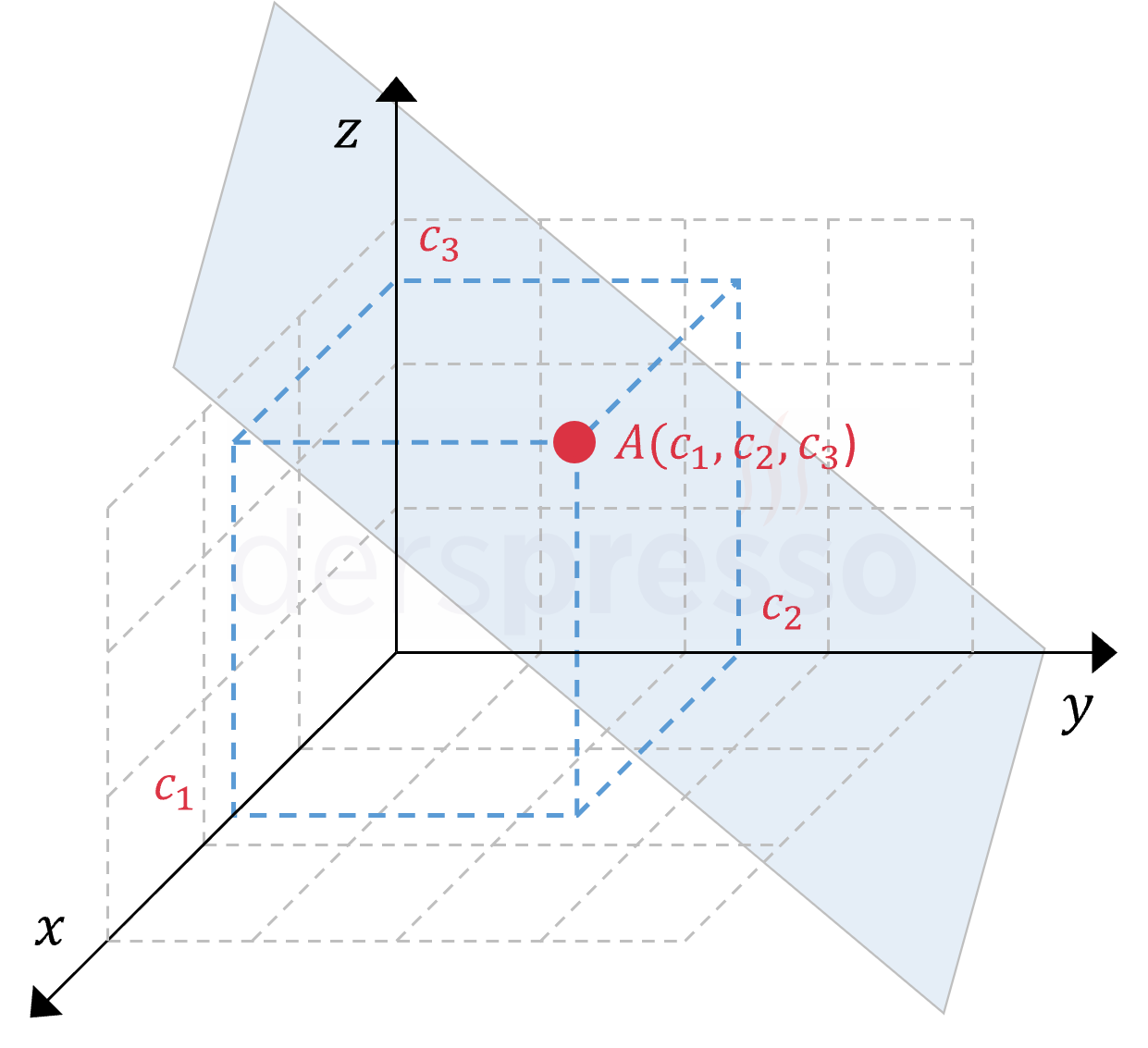
n bilinmeyenli bir lineer denklemin her bir çözümü (x₁,x₂,…,x_n)=(c₁,c₂,…,c_n) şeklinde bir sıralı n’lidir.

Birinci Dereceden Bir Bilinmeyenli Denklemler

Birinci dereceden bir bilinmeyenli denklemler, derecesi bir olan tek bir bilinmeyenden oluşan denklemlerdir.

a,b∈R,a≠0 olmak üzere,

ax+b=0

Bu denklemde x denklemin bilinmeyeni, a ve b denklemin katsayılarıdır. b katsayısı aynı zamanda denklemin sabit terimidir.

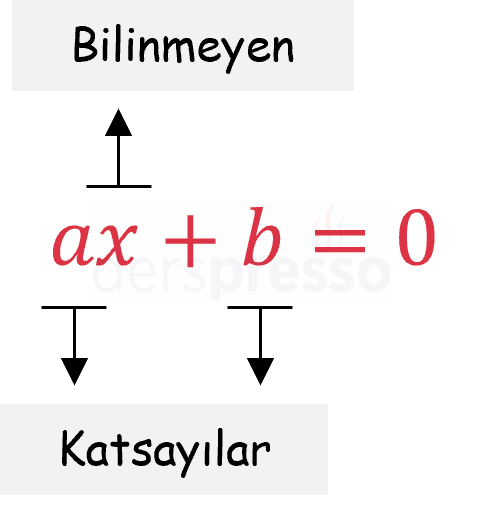
Birinci dereceden bir bilinmeyenli denklemler farklı formlarda olabilir. Aşağıdaki denklemlerin tümünde terimler düzenlendiğinde ilk satırdaki ax+b=0 formundaki 2x−4=0 denklemi elde edilebilir.

2x−4=0

2x=4

4(x−1)=2x

4x+2/2=x+3

ax+b=0 Denkleminin Çözüm Kümesi

ax+b=0 formundaki denklemlerin çözüm kümesi üç farklı şekilde olabilir.

Tek Çözüm

a katsayısının sıfırdan farklı olduğu durumda denklemin tek çözümü olur.

a≠0 ise,

ax+b=0

x=−b/a

Çözüm kümesi: x=−b/a

---

ÖRNEK:

3x−15=0

3x=15

x=5

Çözüm kümesi: x=5

Tüm Reel Sayılar

a ve b katsayılarının ikisinin de sıfır olduğu durumda denklemin tüm reel sayılar olmak üzere sonsuz çözümü olur. a=0 olduğu durumda bu denklemin bir lineer denklem olmayacağını vurgulayalım.

a=b=0 ise,

ax+b=0

0x+0=0

0=0

Çözüm kümesi: x∈R

---

ÖRNEK:

(m−3n)x+2m−5n−2=0

Yukarıdaki denklemin sonsuz çözümünün olması için m ve n değerleri ne olmalıdır?

---

Denklemin sonsuz çözümünün olması için x katsayısı ve sabit terim sıfır olmalıdır.

m−3n=0

⟹m=3n

2m−5n−2=0

⟹6n−5n−2=0

⟹n=2

m=3n=6

(m,n)=(6,2) bulunur.

Bu değerleri denklemde yerine koyalım.

(6−3⋅2)x+2⋅6−5⋅2−2=0

0x+0=0

a ve b katsayılarının ikisi de sıfır olduğunda oluşan 0=0 eşitliği, x bilinmeyeninin alabileceği tüm değerler için, yani x’in değerinden bağımsız olarak eşitliğin sağlanacağını gösterir, dolayısıyla çözüm kümesi tüm reel sayılar olur.

Boş Küme

a katsayısı sıfır, b katsayısı sıfırdan farklı olduğu durumda denklemin çözüm kümesi boş küme olur. Yukarıdaki duruma benzer şekilde, a=0 olduğu durumda bu denklemin bir lineer denklem olmayacağını vurgulayalım.

a=0,b≠0 ise,

ax+b=0

0x+b=0

b=0

b≠0 varsaydığımız için eşitlik hiçbir x değeri için sağlanmaz.

Çözüm kümesi: x∈{}

---

ÖRNEK:

(3m+9)x−m−2n−7=0

Yukarıdaki denklemin çözüm kümesinin boş küme olması için n hangi değeri alamaz?

---

Denklemin çözüm kümesinin boş küme olması için x katsayısı sıfır olmalı ve sabit terim sıfırdan farklı olmalıdır.

3m+9=0

⟹m=−3

−m−2n−7≠0

⟹3−2n−7≠0

⟹n≠−2

Buna göre denklemin çözüm kümesinin boş küme olması için n=−2 değerini alamaz.

b’nin değerini sıfırdan farklı aldığımız için, yukarıda oluşan b=0 eşitliği x’in hiçbir değeri için eşitliğin sağlanmayacağını gösterir, dolayısıyla çözüm kümesi boş küme olur.

Birinci Dereceden Bir Bilinmeyenli Denklemlerin Çözümü

Birinci dereceden bir bilinmeyenli denklemlerin çözümünde bilinmeyen eşitliğin bir tarafında yalnız ve katsayısız bir şekilde bırakılır ve eşitliği sağlayan bilinmeyen değeri bulunur. Bunu sağlarken önceki bölümde gördüğümüz denklem özellikleri kullanılır.

Birinci dereceden bir bilinmeyenli denklemlerin çözüm adımlarını bir örnek üzerinden gösterelim.

ÖRNEK:

Aşağıdaki denklemi sağlayan x değerini bulalım.

3(x+4)−2x+6=−2(x+8)/3

Adım 1: Taraflardan biri kesirli ifade şeklindeyse her iki tarafa aynı çarpma işlemi uygulanarak paydadan kurtulunur. Her iki taraf da kesirli ifade şeklindeyse içler – dışlar çarpımı yapılır.

ÖRNEK (devam):

Denklemin sağ tarafındaki paydadan kurtulmak için her iki tarafı 3 ile çarpalım.

(3(x+4)−2x+6)⋅3=−2(x+8)/3⋅3

3(3(x+4)−2x+6)=−2(x+8)

Adım 2: Eşitliğin her iki tarafındaki parantezli terimler dağıtılır.

ÖRNEK (devam):

Denklemin iki tarafındaki parantezleri dağıtalım.

9(x+4)−6x+18=−2x−16

9x+36−6x+18=−2x−16

Adım 3: Her iki taraftaki benzer terimler kendi aralarında toplanır.

ÖRNEK (devam):

Denklemin sol tarafındaki benzer terimleri toplayalım.

3x+54=−2x−16

Adım 4: Her iki tarafa aynı toplama ve çıkarma işlemleri uygulanarak bilinmeyenli terimler eşitliğin bir tarafında, sabit terimler eşitliğin diğer tarafında toplanır. İşlem kolaylığı açısından bilinmeyenlerin bilinmeyen katsayısının daha büyük olduğu tarafta toplanması tercih edilebilir.

ÖRNEK (devam):

Eşitliğin sağ tarafındaki x’li terimi eşitliğin sol tarafına almak için her iki tarafa 2x ekleyelim.

3x+54+2x=−2x−16+2x

5x+54=−16

Eşitliğin sol tarafındaki sabit terimi eşitliğin sağ tarafına almak için her iki taraftan 54 çıkaralım.

5x+54−54=−16−54

5x=−70

Adım 5: Her iki tarafa aynı çarpma ve bölme işlemleri uygulanarak bilinmeyenin katsayısı 1’e getirilir. Bu adım sonucunda bulunan değer denklemin olası bir çözümüdür.

ÖRNEK (devam):

x’in katsayısını 1’e getirmek için her iki tarafı 5’e bölelim.

5x/5=−70/5

x=−14

Birinci Dereceden İki Bilinmeyenli Denklemler

Birinci dereceden iki bilinmeyenli denklemler, dereceleri bir olan iki bilinmeyenden oluşan denklemlerdir.

a,b,c∈R,a≠0,b≠0 olmak üzere,

ax+by+c=0

Yukarıdaki denklemde x ve y denklemin bilinmeyenleri, a, b ve c denklemin katsayılarıdır. c katsayısı aynı zamanda denklemin sabit terimidir.

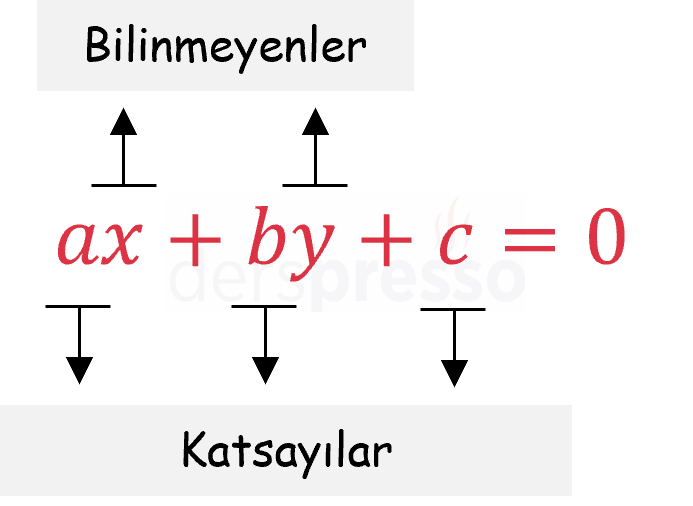
Birinci dereceden iki bilinmeyenli denklemler farklı formlarda olabilir. Aşağıdaki denklemlerin tümünde terimleri düzenlediğimizde ilk satırdaki ax+by+c=0 formundaki 2x−y+4=0 denklemi elde edilebilir.

2x−y+4=0

2x−y=−4

y=2x+4

y/4−x/2=1

Birinci Dereceden İki Bilinmeyenli Denklemlerin Çözüm Kümesi

Birinci dereceden iki bilinmeyenli bir denklemin sonsuz sayıda çözümü vardır ve çözüm kümesi koordinat düzleminde bir doğruya karşılık gelir. Bu doğru üzerindeki her nokta ve karşılık geldiği (x,y) sıralı ikilisi denklemin bir çözümüdür.

ÖRNEK:

3x+2y−24=0 denkleminin çözüm kümesini bulalım.

---

Verilen denklemin analitik düzlemde grafiğini çizelim.

Bu doğru üzerindeki tüm noktalar denklemin birer çözümüdür, yani doğru üzerindeki herhangi bir noktanın karşılık geldiği (x,y) değerleri denklemde yerine konduğunda denklemi sağlar. Benzer şekilde doğru üzerinde olmayan bir noktanın karşılık geldiği (x,y) değerleri denklemde yerine konduğunda denklemi sağlamaz.

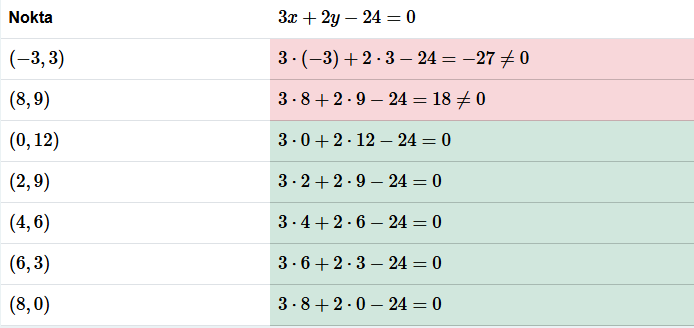
Bu örnek bize birinci dereceden iki bilinmeyenli denklemlerin çözüm kümesinin sonsuz elemanlı olduğunu ve çözüm kümesinin koordinat düzleminde bir doğruya karşılık geldiğini göstermektedir.

SORU 1 :

mx+8=−2y

6x−4y=−n

denklem sisteminin çözüm kümesi sonsuz elemanlı olduğuna göre, m+n kaçtır?

ÇÖZÜM:
mx+2y+8=0

6x−4y+n=0

Birinci dereceden iki bilinmeyenli iki denklemden oluşan denklem sisteminin çözüm kümesi sonsuz elemanlı ise bu denklemlerin temsil ettiği doğrular çakışıktır, dolayısıyla katsayılarının oranları birbirine eşittir.

a1x+b1y+c1=0

a2x+b2y+c2=0

a1/a2=b1/b2=c1/c2

Verilen denklemlerin katsayılarına bu eşitliği uygulayalım.

m/6=2/−4=8/n

m=−3 , n=−16

m+n=−3 + (−16)=−19 bulunur.

SORU 2 :
3x+1=−ay

ax+12y=−2

denklem sisteminin çözüm kümesi boş küme olduğuna göre, a kaçtır?

ÇÖZÜM:
3x+ay+1=0

ax+12y+2=0

Birinci dereceden iki bilinmeyenli iki denklemden oluşan denklem sisteminin çözüm kümesi boş küme ise bu denklemlerin temsil ettiği doğrular paraleldir, dolayısıyla x ve y katsayılarının oranları birbirine eşitken sabit terimlerinin oranları farklıdır.

a1x + b1y + c1 = 0

a2x + b2y + c2 = 0

a1/a2 = b1/b2 ≠ c1/c2

Verilen denklemlerin katsayılarına bu eşitliği/eşitsizliği uygulayalım.

3/a = a/12 ≠ 1/2

a²=36 ⟹ a=±6

a/12 ≠ 1/2 ⟹ a≠6

a=−6 bulunur.

Birinci Dereceden Denklem Sistemleri

Aynı bilinmeyenleri içeren, iki ya da daha fazla denklemden oluşan ve tüm denklemleri birlikte sağlayan bir çözümü bulunmaya çalışılan denklem grubuna denklem sistemi denir.

İki bilinmeyen ve iki denklemden oluşan aşağıdaki denklem sistemini birinci dereceden denklem sistemlerine örnek olarak verebiliriz.

{3x+2y−24=0 x−y+7=0

(x,y)=(4,6) ikilisinin bu denklem sisteminin bir çözümü olabilmesi için sistemdeki iki denklemi de sağlaması gerekir. Bu değerleri denklemlerde yerine koyarak eşitliklerin sağlanıp sağlanmadığını kontrol edelim.
x=4 ve y=6 için:

3⋅4+2⋅6−24=0

4−6+7=5≠0

Buna göre (4,6) ikilisi birinci denklemin bir çözümüdür, ama ikinci denklemin bir çözümü değildir. Her iki denklem birlikte sağlanmadığı için (4,6) ikilisi bu denklem sisteminin bir çözümü değildir.

Şimdi de (x,y)=(2,9) sıralı ikilisinin bu denklem sisteminin bir çözümü olup olmadığına bakalım.
x=2 ve y=9 için:

3⋅2+2⋅9−24=0

2−9+7=0

Her iki denklem birlikte sağlandığı için (2,9) ikilisi bu denklem sisteminin bir çözümüdür.

Buna göre n denklemden oluşan bir denklem sisteminin çözüm kümesi sistemdeki denklemlerin ayrı ayrı çözüm kümelerinin kesişim kümesine eşittir.

ÇK=ÇK1∩ÇK2∩…∩ÇKn

Birinci Dereceden Denklem Sistemlerinin Çözümü

Birinci dereceden denklem sistemlerinin çözümünde kullanabileceğimiz bazı yöntemler aşağıdaki gibidir.

Yerine Koyma Yöntemi:

Bu yöntemde bilinmeyenlerden biri herhangi bir denklemde yalnız bırakılır, sonra eşit olduğu ifade ikinci denklemde yerine konur ve ikinci denklem bir bilinmeyenli denklem şeklinde çözülür.

Yerine koyma yönteminin adımlarını yukarıda kullandığımız örnek üzerinden gösterelim.

{3x+2y−24=0 , x−y+7=0

Adım 1: Bilinmeyenlerden biri herhangi bir denklemde yalnız bırakılarak diğer bilinmeyen cinsinden yazılır.

İkinci denklemde y bilinmeyenini yalnız bırakalım.

x−y+7=0

y=x+7

Adım 2: Elde edilen eşitlik diğer denklemde yerine konur ve bu denklem bir bilinmeyenli denklem şeklinde çözülür.

Elde ettiğimiz eşitliği birinci denklemde y yerine koyalım.

3x+2y−24=0

3x+2(x+7)−24=0

3x+2x+14−24=0

5x=10

x=2

Adım 3: Bulunan değer orijinal denklemlerden birinde yerine konur ve diğer bilinmeyenin değeri bulunur.

İkinci denklemde x=2 koyarak y değerini bulalım.

x−y+7=0

2−y+7=0

y=9

Denklem sisteminin çözümünü yukarıda sağlamasını yapmış olduğumuz gibi (x,y)=(2,9) olarak bulmuş olduk.

x=2 değerini birinci denklemde yerine koymuş olsaydık da aynı y değerini elde edeceğimizi teyit edelim.

3x+2y−24=0

3⋅2+2y−24=0

2y=18

y=9

Bu yöntemde ilk adımda hangi denklemdeki hangi bilinmeyeni yalnız bırakırsak bırakalım aynı sonucu elde ederiz.

Bir denklem sistemindeki denklemlerden biri y=ax+b formunda ise yerine koyma yöntemi daha hızlı sonuç verecektir.

Yok Etme (Eliminasyon) Yöntemi:

Bu yöntemde denklemler bilinmeyenlerden birinin katsayıları birbirini götürecek ve bir bilinmeyenli bir denklem elde edilecek şekilde düzenlenir ve taraf tarafa toplanır.

Yok etme yönteminin adımlarını aynı örnek üzerinden gösterelim.

{3x+2y−24=0 , x−y+7=0

Adım 1: Yok edilecek bilinmeyen seçilir.

Bu örnekte x bilinmeyenini yok edelim.

Adım 2: Her iki denklemde seçilen bilinmeyenin katsayıları birbirinin toplamaya göre tersi olacak şekilde denklemlerden birinin ya da ikisinin tarafları sabit sayılarla çarpılır.

x bilinmeyeninin birinci denklemde katsayısı 3, ikinci denklemde 1’dir.

Bu katsayıları birbirinin toplamaya göre tersi yapmak için ikinci denklemin taraflarını −3 ile çarpalım.

−3(x−y+7)=−3⋅0

−3x+3y−21=0

Adım 3: Denklemler taraf tarafa toplanır ve seçilen bilinmeyenin toplam satırında birbirini götürmesi sağlanır.

İki denklemi taraf tarafa toplayalım.

3x+2y−24=0

−3x+3y−21=0

==================

0x+5y−45=0

5y−45=0

Adım 4: Elde edilen tek bilinmeyenli denklem çözülür.

y bilinmeyenini yalnız bırakalım.

5y−45=0

5y=45

y=9

Adım 5: Bulunan değer orijinal denklemlerden birinde yerine konur ve diğer bilinmeyenin değeri bulunur.

Bulduğumuz y değerini ikinci denklemde yerine koyalım.

x−y+7=0

x−9+7=0

x=2

Denklem sisteminin çözümünü diğer yöntemde olduğu gibi (x,y)=(2,9) olarak bulmuş olduk.

Bir denklem sistemindeki denklemlerin tümü ax+by+c=0 formunda ise yok etme yöntemi daha hızlı sonuç verecektir.

Eşitleme Yöntemi:

Bu yöntemde her iki denklemde aynı bilinmeyen yalnız bırakılır ve bu bilinmeyenin eşit olduğu ifadeler birbirine eşitlenir.

Eşitleme yönteminin adımlarını aynı örnek üzerinden gösterelim.

{3x+2y−24=0 , x−y+7=0

Adım 1: Yalnız bırakılacak bilinmeyen seçilir.

Bu örnekte x bilinmeyenini yalnız bırakalım.

Adım 2: Her iki denklemde bu bilinmeyen yalnız bırakılır.

Birinci denklemde x’i yalnız bırakalım.

x=−2/3y+8

İkinci denklemde x’i yalnız bırakalım.

x=y−7

Adım 3: Yalnız bırakılan bilinmeyenin eşit olduğu iki ifade birbirine eşitlenir.

İki denklemde x’in eşit olduğu ifadeleri eşitleyelim.

x=x

−2/3y+8=y−7

Adım 4: Elde edilen bir bilinmeyenli denklem çözülür.

y’li terimleri eşitliğin sol tarafında, sabit terimleri sağ tarafında toplayalım.

−5/3y=−15

y=9

Adım 5: Bulunan değer orijinal denklemlerden birinde yerine konur ve diğer bilinmeyenin değeri bulunur.

Bulduğumuz y değerini ikinci denklemde yerine koyalım.

x−y+7=0

x−9+7=0

x=2

Bir denklem sistemindeki denklemlerin tümü y=ax+b formunda ise eşitleme yöntemi daha hızlı sonuç verecektir.

Grafik Yöntemi:

Önceki bölümde gördüğümüz üzere, birinci dereceden iki bilinmeyenli bir denklemin grafiği bir doğrudur ve bu doğrunun üzerindeki tüm noktalar denklemin birer çözümüdür. Bir denklem sisteminde ise sistemdeki tüm denklemlerin grafiklerinin (varsa) kesişim noktası denklem sisteminin çözümünü verir. Buna göre doğrular tek bir noktada kesişiyorsa denklem sisteminin tek bir çözümü vardır, doğrular paralel ise (kesişmiyor ise) denklem sisteminin bir çözümü yoktur, doğrular çakışık ise denklem sisteminin sonsuz çözümü vardır.

Yukarıda kullandığımız denklem sistemindeki iki denklemin grafiklerini çizelim.

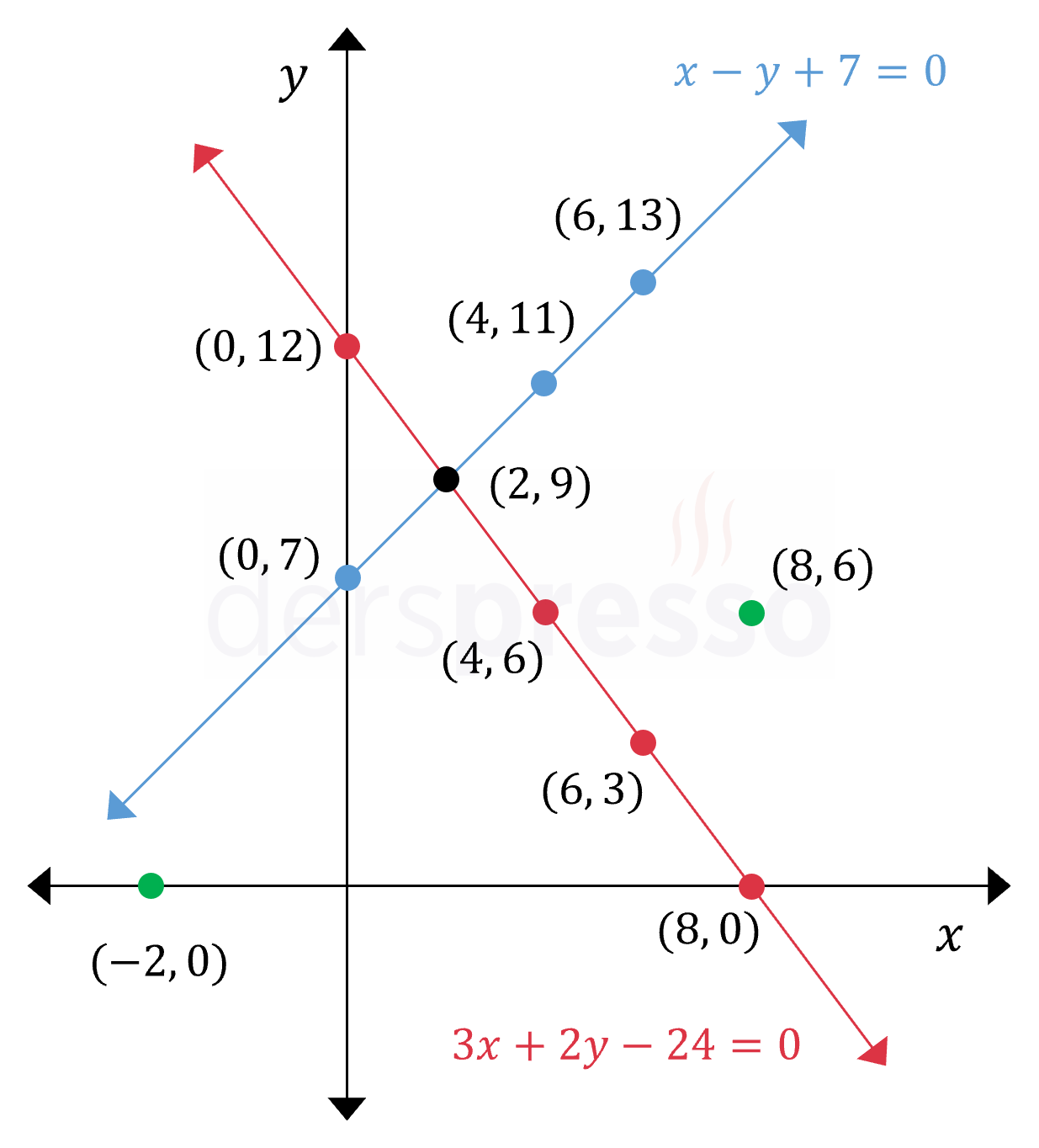
1. dereceden iki bilinmeyenli denklem sisteminin grafiği

Denklem grafiklerinde işaretli bazı noktaların iki denklemi sağlama durumları aşağıdaki gibidir.

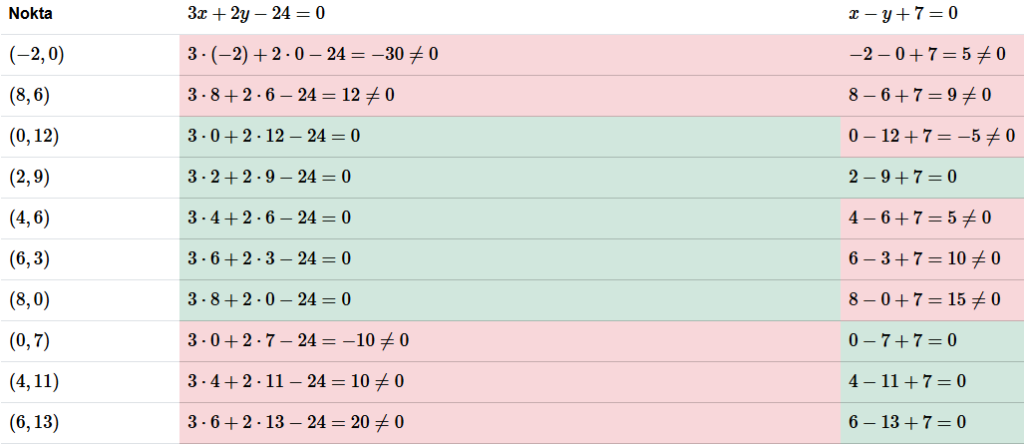
Bu grafiği ve tabloyu aşağıdaki şekilde yorumlayabiliriz.

• Her noktanın ilgili denklemi sağladığı durumlar yeşil, sağlamadığı durumlar pembe ile tabloda işaretlenmiştir.
• Bir nokta bir denklemin grafiği üzerindeyse o denklemi sağlamakta, değilse sağlamamaktadır.
• Her iki doğrunun da üzerinde olmayan iki nokta ((−2,0) ve (8,6)) iki denklemi de sağlamamaktadır.
• Her iki doğrunun kesişimi olan nokta ((2,9)) her iki denklemi de sağlamaktadır.

Özetlemek gerekirse, bir denklemin çözüm kümesi o denklemin grafiği üzerindeki tüm noktalardır. Bir denklem sisteminin çözüm kümesi ise denklem sistemindeki denklemlerin grafiklerinin (varsa) kesişim noktası ya da noktalarıdır.

Birinci Dereceden Eşitsizlikler

Derecesi (kuvveti) bir olan bilinmeyenlerden oluşan ve aşağıdaki şekilde ifade edilebilen eşitsizliklere birinci dereceden eşitsizlik denir. Aşağıdaki tanımda kullanılan < sembolü yerine diğer ≤, >, ≥ sembolleri de kullanılabilir.

a1,a2,…,an ∈ R

(a1,a2,…,an)≠(0,0,…,0) olmak üzere,

a1x1+a2x2+…+anxn+b<0

---

ÖRNEK:

3x+5<−4

−2x+5y≥3

x+2y+3z<15

Bu eşitsizlikte x₁,x_2,…,x_n eşitsizliğin bilinmeyenleri, a₁,a₂,…,a_n ve b eşitsizliğin katsayılarıdır. b katsayısı aynı zamanda eşitsizliğin sabit terimidir.

Her ne kadar birinci dereceden eşitsizlikler birinci dereceden denklemler gibi n bilinmeyenli olabilse de, daha fazla bilinmeyenli eşitsizlikler daha ileri çözüm teknikleri gerektirdiği için karşılacağımız çoğu eşitsizlik bir ya da iki bilinmeyenli olacaktır.

Birinci Dereceden Bir Bilinmeyenli Eşitsizlikler

Birinci dereceden bir bilinmeyenli eşitsizlikler aşağıdaki formlarda olabilir ve farklı eşitsizlik sembolleri (<,≤,>,≥) içerebilir.

a,b∈R,a≠0 olmak üzere,

ax+b<n

m<ax+b

m<ax+b<n

Birinci dereceden bir bilinmeyenli eşitsizliklerin çözümünde bilinmeyen katsayısız bir şekilde yalnız bırakılır ve eşitsizliği sağlayan değer aralığı bulunur. Bunu sağlarken önceki bölümde gördüğümüz eşitsizlik özellikleri kullanılır.

Birinci dereceden bir bilinmeyenli eşitsizliklerin çözüm adımlarını bir örnek üzerinden gösterelim.

ÖRNEK 1:

Aşağıdaki eşitsizliği sağlayan x değer aralığını bulalım.

−8≤3(x+5)−2/4<7

---

Aynı işlemleri eşitsizliğin taraflarına adım adım uygulayarak x’i yalnız bırakalım.

Tüm tarafları 4 ile çarpalım.

4⋅(−8)≤4⋅3(x+5)−2/4<4⋅7

−32≤3(x+5)−2<28

Tüm taraflara 2 ekleyelim.

−32+2≤3(x+5)−2+2<28+2

−30≤3(x+5)<30

Tüm tarafları 3’e bölelim.

−30/3≤3(x+5)/3<30/3

−10≤x+5<10

Tüm taraflardan 5 çıkaralım.

−10−5≤x+5−5<10−5

−15≤x<5

Bir bilinmeyenli eşitsizlikler aşağıdaki formda, yani eşitsizliğin birden fazla tarafı aynı değişkeni içerecek şekilde de olabilir. Bu tip eşitsizlikler iki eşitsizliğe bölünerek ve her eşitsizliğin çözümünden elde edilen çözüm aralıklarının kesişim kümesi alınarak çözülür.

a₁x+b₁<a₂x+b₂<a₃x+b₃

⟹a₁x+b₁<a₂x+b₂

⟹a₂x+b₂<a₃x+b₃

---

ÖRNEK 2:

5x−1≤4x+8<7x−13 eşitsizliğinin çözüm kümesini bulalım.

---

5x−1≤4x+8 eşitsizliğini çözelim.

Bilinmeyenleri eşitsizliğin sol tarafında, sabit terimleri sağ tarafında toplayalım.

5x−4x≤8+1

x≤9

4x+8<7x−13 eşitsizliğini çözelim.

Bilinmeyenleri eşitsizliğin sağ tarafında, sabit terimleri sol tarafında toplayalım.

8+13≤7x−4x

21≤3x

7≤x

Verilen eşitsizliğin çözüm kümesi elde ettiğimiz iki aralığın kesişim kümesidir.

7≤x≤9

---

ÖRNEK 3:

2m+3<83≤5m−7 olduğuna göre, m değer aralığını bulalım.

---

Eşitsizliği iki ayrı eşitsizliğe bölerek ayrı ayrı çözelim.

2m+3<83 ve 83≤5m−7

2m+3<83 eşitsizliğini çözelim.

Eşitsizliğin taraflarından 3 çıkaralım.

2m+3−3<83−3

2m<80

Eşitsizliğin taraflarını 2’ye bölelim.

2m/2<80/2

m<40

83≤5m−7 eşitsizliğini çözelim.

Eşitsizliğin taraflarına 7 ekleyelim.

83+7≤5m−7+7

90≤5m

Eşitsizliğin taraflarını 5’e bölelim.

90/5≤5m/5

18≤m

m değer aralığı iki eşitsizlikte bulduğumuz değer aralıklarının kesişim kümesidir.

18≤m<40

Birinci Dereceden İki Bilinmeyenli Eşitsizlikler

Birinci dereceden iki bilinmeyenli eşitsizlikler aşağıdaki formda olurlar ve farklı eşitsizlik sembolleri (<,≤,>,≥) içerebilir.

a,b,c∈R olmak üzere,

ax+by+c<0

Analitik düzlemde belirli bir denklemin çözüm kümesi o denklemin grafiği üzerindeki noktalar kümesidir. Bir eşitsizlik ya da eşitsizlik sisteminin çözüm kümesi ise genellikle analitik düzlemde bir bölgeye karşılık gelir.

Eşitsizliklerin Analitik Gösterimi

Bir noktanın bir doğruya (ya da herhangi bir fonksiyona) göre konumunu üç farklı şekilde düşünebiliriz. Buna göre nokta doğrunun üzerinde olabilir (A noktası), üstündeki bölgede olabilir (B noktası) ya da altındaki bölgede olabilir (C noktası).

Noktanın doğruya göre durumu

Belirli bir noktanın bir doğruya göre konumunu bulmak için noktanın koordinatları doğrunun y=ax+b şeklindeki açık denkleminde yerine konur ve oluşan ifadenin tarafları arasındaki eşitlik ya da eşitsizlik durumu incelenir.

y₁=ax₁+b⟹ Nokta doğrunun üzerindedir (A noktası)

y₂>ax₁+b⟹ Nokta doğrunun üstündeki bölgededir (B noktası)

y₃<ax₁+b⟹ Nokta doğrunun altındaki bölgededir (C noktası)

---

ÖRNEK:

A(12,60) noktasının y=8x−15 doğrusuna göre konumunu bulalım.

A noktasının koordinatlarını denklemde yerine koyalım ve taraflar arasında oluşan eşitlik ya da eşitsizlik durumunu inceleyelim.

60⋚?8⋅12−15

60<81

Buna göre A noktası verilen doğrunun altındaki bölgededir.

Bunun bir sonucu olarak, bir doğrunun (ya da herhangi bir fonksiyonun) analitik düzlemde oluşturduğu bölgeler ve bu bölgelerin karşılık geldiği eşitlik ya da eşitsizlikler aşağıdaki gibi olur.

Grafik	Eşitlik/Eşitsizlik
	y=ax+bDoğrunun üzerindeki noktalar
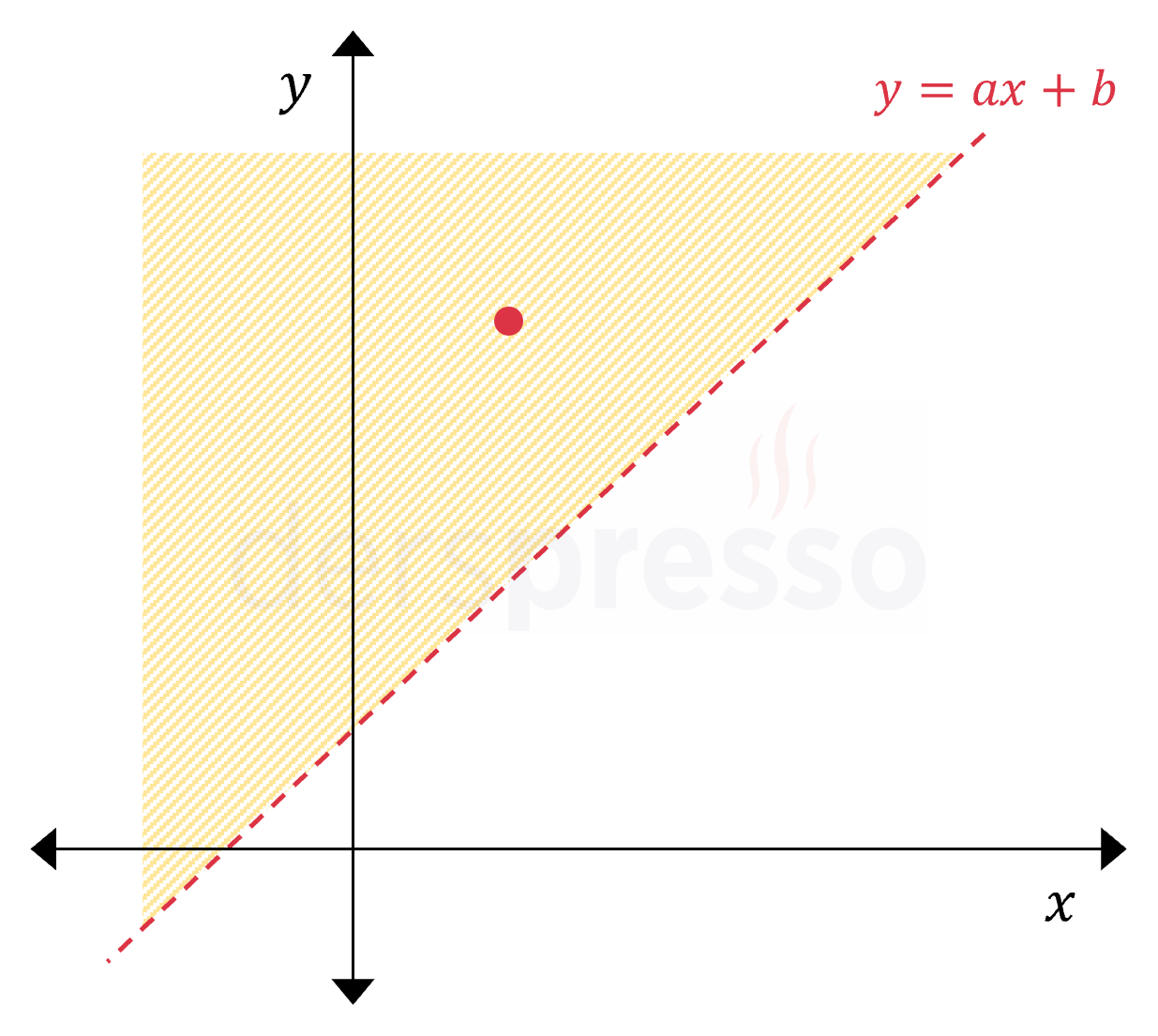	y>ax+bDoğrunun üstündeki bölgedeki noktalar> eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olmadığını vurgulamak için doğru kesikli çizgi ile gösterilir.
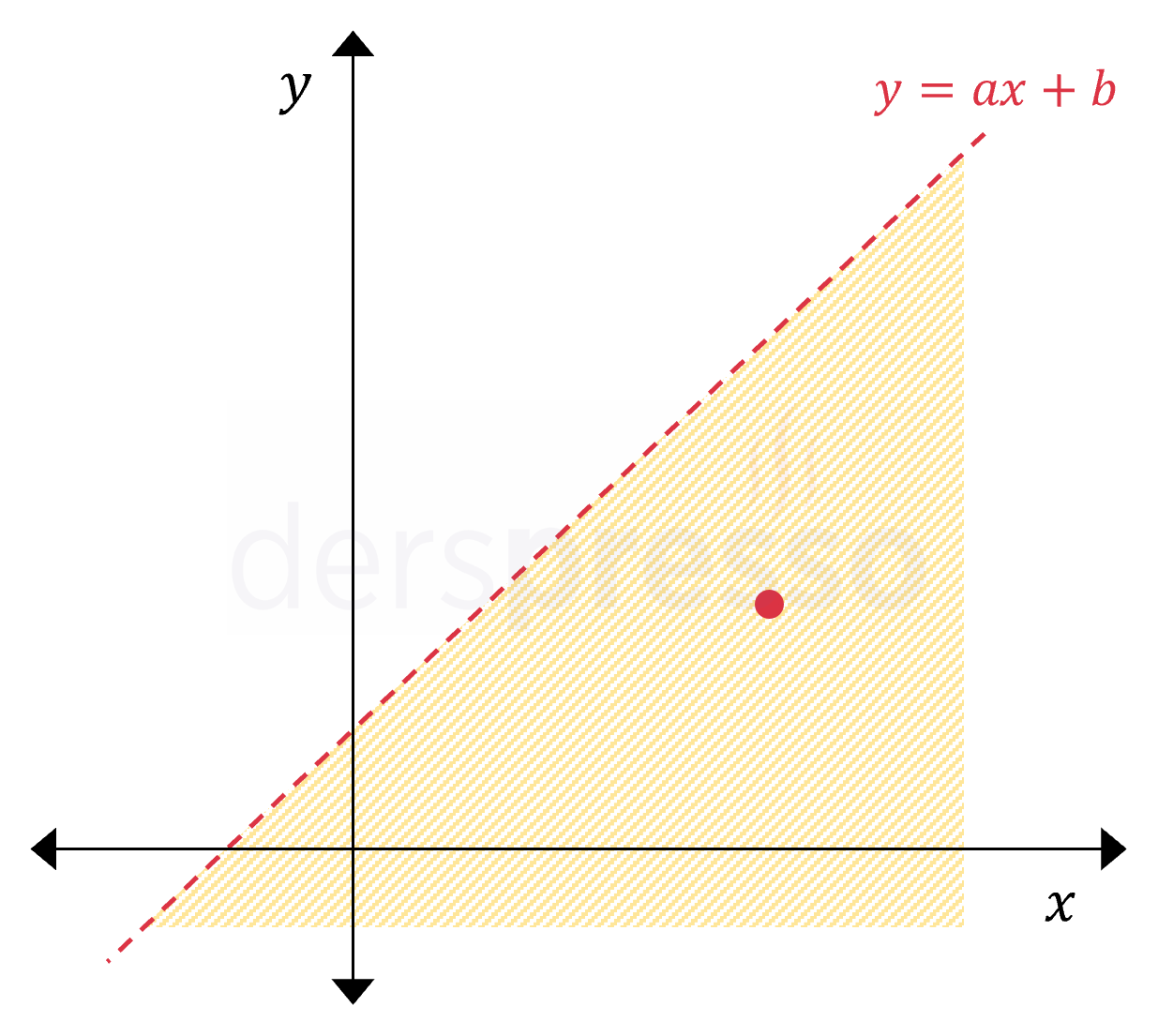	y<ax+bDoğrunun altındaki bölgedeki noktalar< eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olmadığını vurgulamak için doğru kesikli çizgi ile gösterilir.
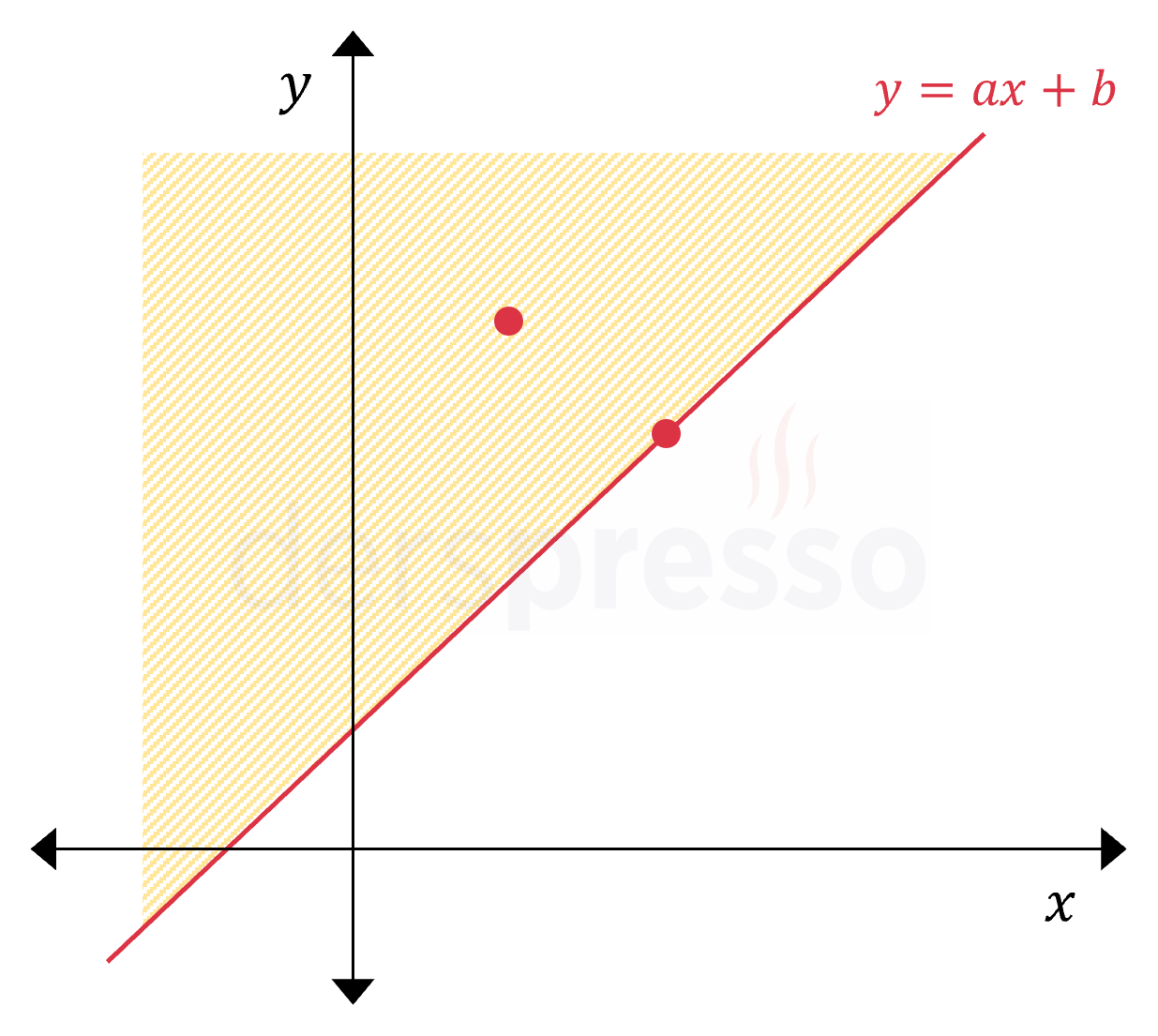	y≥ax+bDoğrunun üzerindeki ve üstündeki bölgedeki noktalar≥ eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olduğunu vurgulamak için doğru sürekli çizgi ile gösterilir.
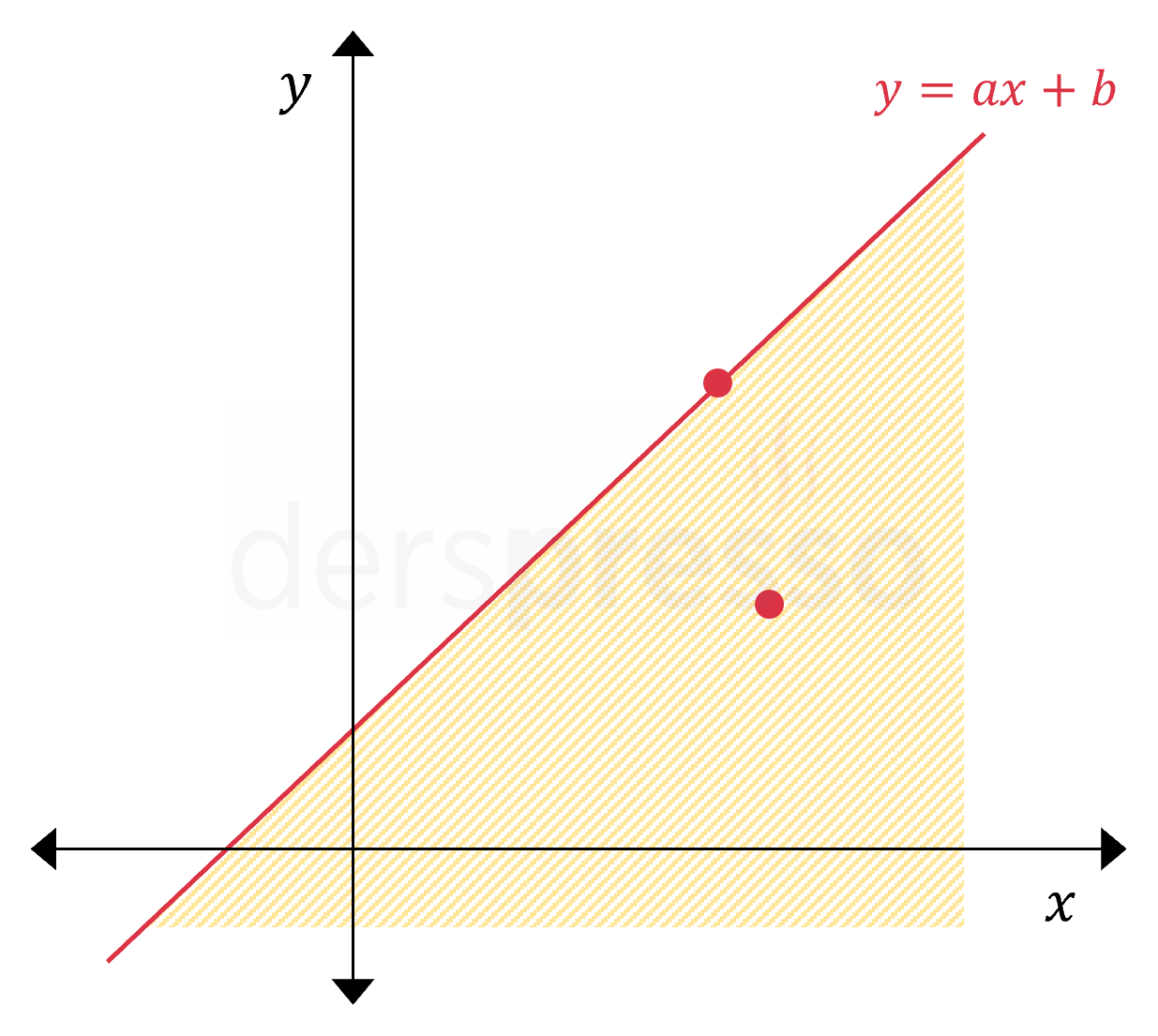	y≤ax+bDoğrunun üzerindeki ve altındaki bölgedeki noktalar≤ eşitsizliğinde doğrunun üzerindeki noktaların çözüm kümesine dahil olduğunu vurgulamak için doğru sürekli çizgi ile gösterilir.

Aşağıda örnek bazı doğrusal eşitsizlikler ve analitik düzlemde karşılık geldikleri bölgeler gösterilmiştir.

Eşitsizliklerin Analitik Düzlemde Gösterimi

y⋚ax+b şeklindeki bir eşitsizliğin analitik düzlemde temsil ettiği bölgeyi aşağıdaki şekilde gösterebiliriz.

• y=ax+b doğrusu çizilir. Eşitsizlik sembolü ≥ ya da ≤ ise doğru sürekli bir çizgi ile, > ya da < ise kesikli bir çizgi ile çizilir.
• Eşitsizlik sembolü ≥ ya da > ise doğrunun üstünde kalan, ≤ ya da < ise altında kalan bölge taranır.
• Özel bir durum olarak, eğer denklem x=b şeklinde dikey bir doğru ise x>b için doğrunun sağındaki, x<b için solundaki bölge taranır.

SORU:
3y−x…6

ifadesinde verilen boşluğa hangi eşitlik ya da eşitsizlik sembolü gelirse oluşan ifadenin grafiği (1,2) noktasını içerir?

ÇÖZÜM:

Bir eşitsizliğin grafiği bir noktayı içeriyorsa o nokta eşitsizliği sağlamalıdır.

Eşitsizlikte (x,y) değerleri yerine (1,2) koyalım.

3⋅2−1…6

5…6

Bu ifadenin doğru olması için boşluğa < gelmelidir.

5<6

Eşitsizlik Sistemlerinin Gösterimi

Eşitsizlik sistemleri birden fazla eşitsizlikten oluşur ve çözüm kümeleri tüm eşitsizlikleri birlikte sağlayan noktaları içerir. Bir diğer ifadeyle, bir eşitsizlik sisteminin karşılık geldiği taralı bölge, sistemi oluşturan eşitsizliklerin ayrı ayrı taradıkları alanların kesişim kümesidir.

Aşağıda örnek bazı eşitsizlik sistemleri ve analitik düzlemde karşılık geldikleri bölgeler gösterilmiştir.

Grafik	Eşitsizlik Sistemi
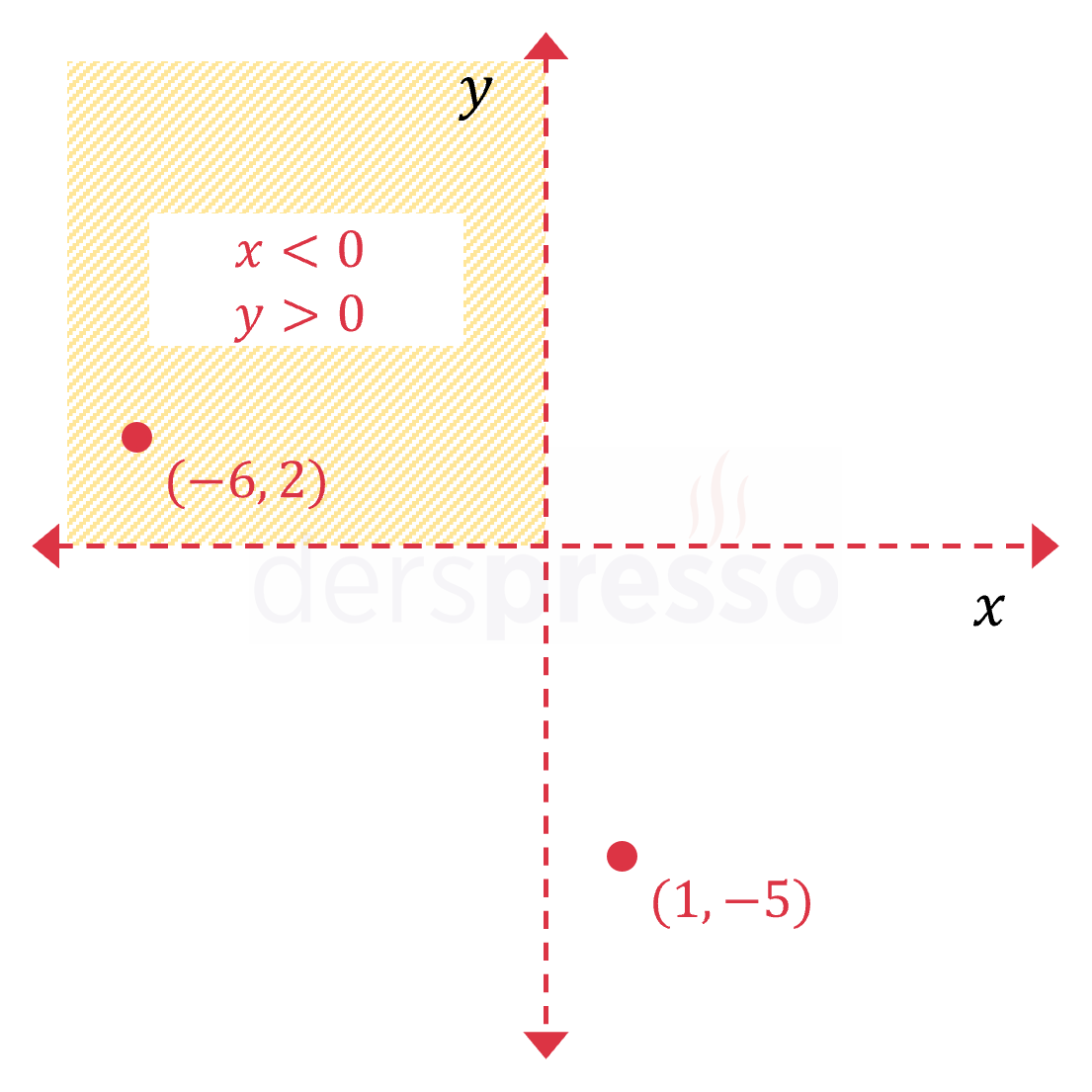	{x<0y>0Bu eşitsizlik sistemi apsis değeri negatif ve ordinat değeri pozitif olan noktaları içerir.Kesikli çizgi ile gösterilen x ve y eksenleri, üzerlerindeki noktaların eşitsizliğe dahil olmadığını gösterir.(−6,−2) noktası eşitsizliklerin tümünü sağladığı için taralı bölgeye dahildir. (1,−5) noktası eşitsizliklerin tümünü sağlamadığı için taralı bölgeye dahil değildir.
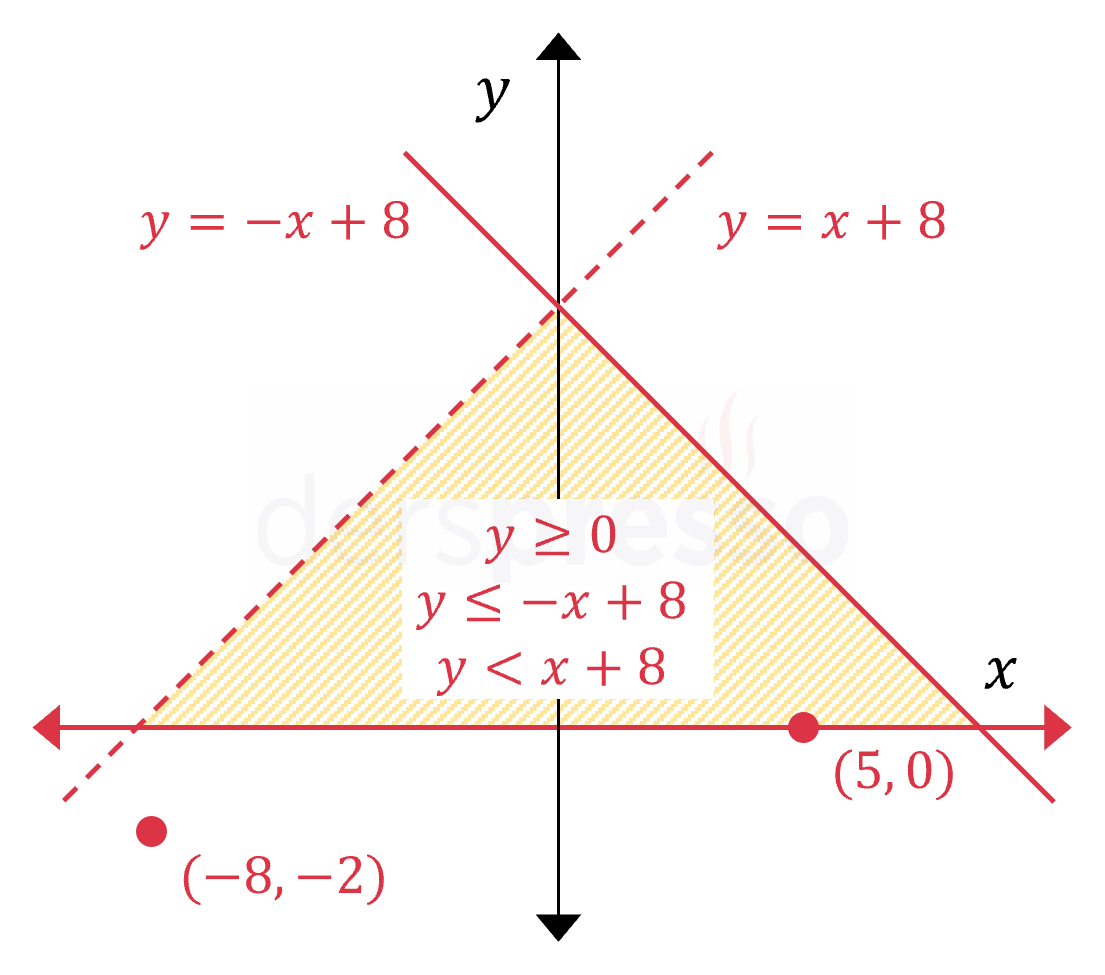	{y≥0y≤−x+8y<x+8Sürekli çizgi ile gösterilen x ekseni ve y=−x+8 doğrusu, üzerlerindeki noktaların eşitsizliğe dahil olduğunu gösterir. Kesikli çizgi ile gösterilen y=x+8 doğrusu, üzerindeki noktaların eşitsizliğe dahil olmadığını gösterir.(5,0) noktası eşitsizliklerin tümünü sağladığı için taralı bölgeye dahildir. (−8,−2) noktası eşitsizliklerin tümünü sağlamadığı için taralı bölgeye dahil değildir.
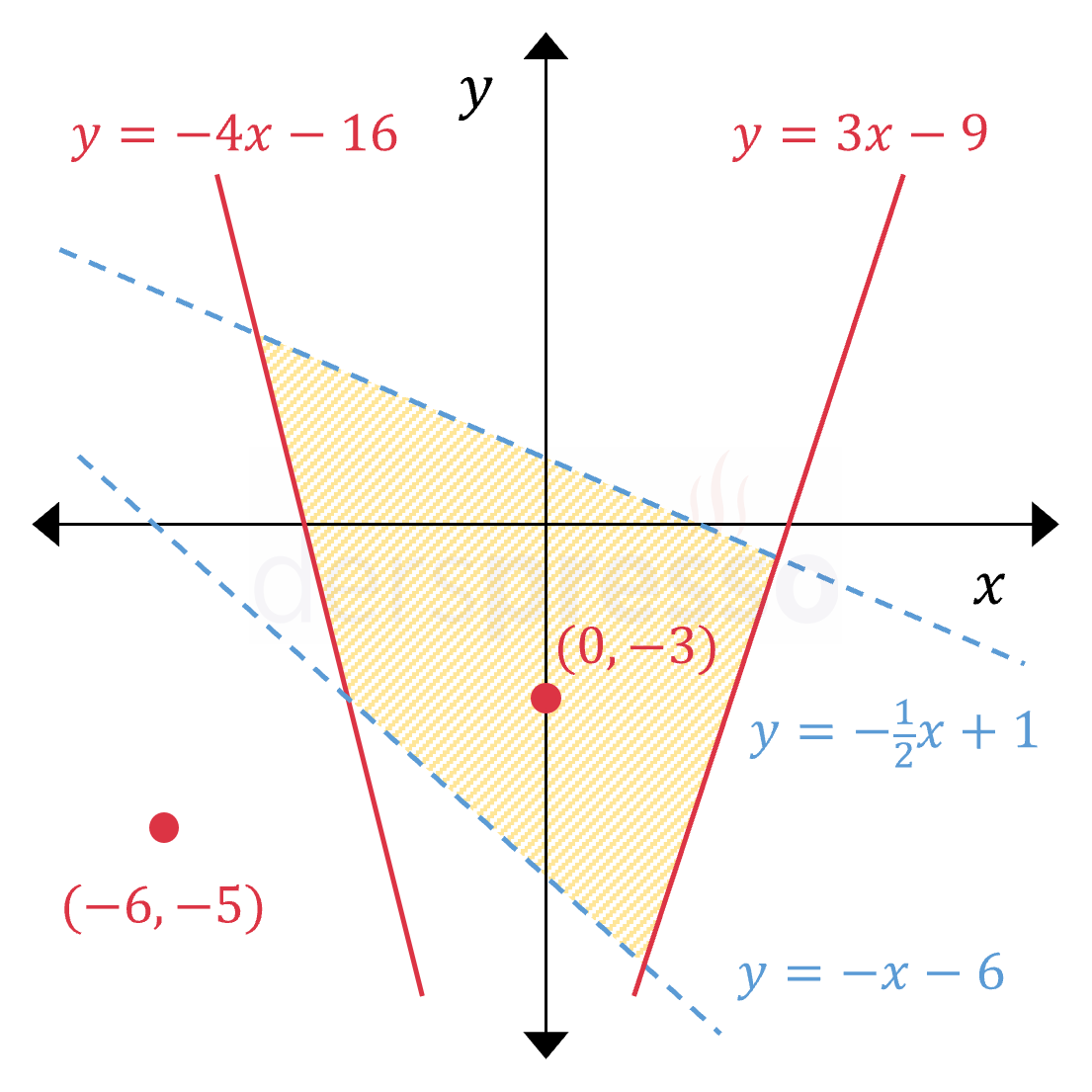	{y≥3x−9y≥−4x−16y<−12x+1y>−x−6Sürekli çizgi ile gösterilen y=3x−9 ve y=−4x−16 doğruları, üzerlerindeki noktaların eşitsizliğe dahil olduğunu gösterir. Kesikli çizgi ile gösterilen y=−12x+1 ve y=−x−6 doğruları, üzerlerindeki noktaların eşitsizliğe dahil olmadığını gösterir.(0,−3) noktası eşitsizliklerin tümünü sağladığı için taralı bölgeye dahildir. (−6,−5) noktası eşitsizliklerin tümünü sağlamadığı için taralı bölgeye dahil değildir.