1. Konunun Tanımı

Sayı ve kesir problemleri, sayılar arasındaki ilişkileri ve kesirlerin kullanımıyla ilgili matematiksel işlemleri içeren problemlerdir. TYT matematikte önemli bir yer tutar ve temel matematik becerilerini geliştirir. Sayı ve kesir problemleri, genellikle mantıksal düşünme, işlem yeteneği ve problem çözme stratejileri gerektiren konular arasında yer alır.

Bu problemler, günlük hayatta karşılaşılan birçok matematiksel durumun anlaşılması ve çözümüne katkı sağlar. Alışveriş yaparken, yemek tariflerinde malzemeleri oranlarken, zaman hesaplamalarında ve mühendislik alanında kullanılan hesaplamalarda sayı ve kesirler önemli bir yer tutar.

---

2. Sayı Problemleri

2.1. Sayılar Arasındaki İlişkiler

• Ardışık Sayılar: Belirli bir kurala göre sıralanan sayı dizileri olup, özellikle tek ve çift sayılar üzerine kurulu sorular sıkça karşılaşılır.
• Rakamları Toplamı Verilen Sayılar: Sayının rakamlarının toplamını kullanarak sayıyı belirleme veya sayıya ilişkin özel durumları çözme yöntemleri.
• Sayıların Çarpanları ve Bölenleri: Bir sayının bölenlerini bulma, asal çarpanlara ayırma ve EBOB-EKOK problemleri.
• Mutlak Değer Problemleri: Bir sayının sıfırdan uzaklığını ifade eden mutlak değer kavramı ve buna dayalı sorular.
• Modüler Aritmetik: Bir sayının belirli bir sayıya bölündüğünde kalanını gösteren modüler aritmetik yöntemleri ve uygulamaları.
• Üslü ve Köklü Sayılar: Üstel ifadeler ve karekök kavramlarıyla ilgili problemler.

Örnek Problem:

İki ardışık tek sayının toplamı 48’dir. Bu sayılar nelerdir?
Çözüm: x ve x+2 şeklinde tanımlanır. Denklem kurularak çözülür.

2.2. Basamak Kavramı

• Basamak Değerleri: Bir sayının basamak değerlerinin bilinmesi, problemlerde önemli bir yer tutar.
• Sayının Ters Çevrilmesi: Basamakların yer değiştirmesiyle farklı problemler oluşturulabilir.
• Sayının Çözümlemesi: Sayının basamak değerleri üzerinden ayrıştırılması ve ifade edilmesi.
• Bölünebilme Kuralları: 2, 3, 4, 5, 6, 9 ve 10’a bölünebilme kurallarını kullanarak sayı analizleri yapmak.

Örnek Problem:

İki basamaklı bir sayının onlar basamağı bir artırıldığında sayı 10 artmaktadır. Sayı kaç olabilir?

Çözüm:
İki basamaklı bir sayıyı 10a + b şeklinde ifade edelim.
Burada:

• a → onlar basamağındaki rakam
• b → birler basamağındaki rakam

Soruda verilen bilgiye göre, onlar basamağı 1 artırıldığında sayı 10 artıyor.
Yani yeni sayı 10(a+1) + b olacaktır.

Bu durumda denklemi yazalım:10(a+1)+b=10a+b+10

Şimdi denklemin her iki tarafından 10a + b‘yi çıkaralım:10a+10+b−(10a+b)=10

Buradan:10=10

Bu denklem her zaman doğrudur, yani bütün iki basamaklı sayılar bu şartı sağlar.
Dolayısıyla çözüm kümesi tüm iki basamaklı sayılar (10 ile 99 arasındaki tüm sayılar) olacaktır.

2.3. Yaş Problemleri

• Kişilerin Yaş Farkları: Değişmeyen yaş farklarını kullanarak çözüme ulaşılır.
• Zaman İçinde Değişen Yaş Problemleri: Geçmiş ve gelecek yıllara yönelik hesaplamalar yapılır.
• Anne, Baba ve Çocuk Yaş Problemleri: Aile bireylerinin yaş ilişkileriyle ilgili hesaplamalar içerir.

Örnek Problem:

Anne ve çocuğunun yaşları toplamı 40’tır. 10 yıl sonra annenin yaşı çocuğunun yaşının 3 katı olacaktır. Annelerinin ve çocuklarının şimdiki yaşları nedir?

Çözüm:

• Annenin yaşını A, çocuğun yaşını C olarak tanımlayalım.
• İlk verilen bilgiye göre: A+C=40
• 10 yıl sonra annenin ve çocuğun yaşları sırasıyla A + 10 ve C + 10 olacak.
• Bu durumda: A+10=3×(C+10)

Şimdi bu denklemi çözelim:

1. A + C = 40 denkleminden A = 40 – C yazabiliriz.
2. Bunu ikinci denkleme yerleştirelim: (40−C)+10=3(C+10)
3. 50−C=3C+30
4. 50−30=3C+C
5. 20=4C
6. C=5

Çocuğun yaşı 5 bulunur. Şimdi annenin yaşını bulalım:A=40−5=35

Cevap:
Annenin yaşı 35, çocuğun yaşı 5‘tir.

2.4. Sayıların Bölünebilme Kuralları

• 2, 3, 4, 5, 6, 9 ve 10’a bölünebilme kuralları detaylı açıklanır.
• Sayılardaki bilinmeyenleri bu kuralları kullanarak bulma yöntemleri üzerinde durulur.

---

3. Kesir Problemleri

3.1. Kesirlerin Tanımı ve Türleri

• Basit Kesirler (pay < payda)
• Bileşik Kesirler (pay > payda)
• Tam Sayılı Kesirler (tam sayı ve kesirin birleşimi)
• Kesirleri Ondalık Sayılara Çevirme ve Tersine Dönüştürme

3.2. Kesirlerde Dört İşlem

• Toplama ve Çıkarma: Payda eşitleme yöntemiyle hesaplanır.
• Çarpma ve Bölme: Doğrudan çarpma işlemi yapılırken, bölme işleminde ters çevirme yöntemi kullanılır.
• Kesirlerde Sıralama ve Karşılaştırma: Sayısal büyüklüğe göre sıralama yapılır.

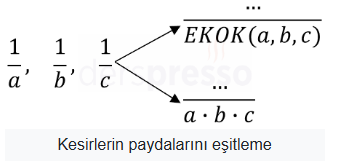
Payda Eşitleme

İki ya da daha fazla kesri, paydaları aynı sayıda buluşacak şekilde genişletme ya da sadeleştirme işlemine payda eşitleme denir. Payda eşitleme kesirler arasındaki toplama, çıkarma ve sıralama işlemlerinde sıklıkla kullanılır.

İki ya da daha fazla kesrin paydalarının eşitlenebileceği en küçük sayı, paydaların ek küçük ortak katıdır (EKOK).

Paydalar EKOK’larının herhangi bir tam sayı katında da eşitlenebilir. Paydaların çarpımı da EKOK’larının bir katı olduğu için paydalar çarpımları olan sayıda da eşitlenebilir.

Kesirlerle Toplama

İki ya da daha fazla kesir arasında toplama işlemi aşağıdaki şekilde yapılır.

• Önce kesirlerin paydaları eşitlenir.
• Paydaları eşitlenmiş kesirlerin paylarının toplamı sonucun payına yazılır.
• Paydaları eşitlenmiş kesirlerin ortak paydası sonucun paydasına aynen taşınır.
• Sonucun pay ve paydası ortak çarpan içeriyorsa sadeleştirme işlemi yapılır.
• Kesirlerden biri ya da birkaçı tam sayılı kesir ise bu kesirlerin tam sayı kısımları kendi aralarında toplanır ve sonucun tam sayı kısmına yazılır. İşlem sonucu bir bileşik kesir ise istenirse sonuç tam sayılı kesre çevrilebilir.

Kesirlerle Çıkarma

İki kesir arasında çıkarma işlemi aşağıdaki şekilde yapılır.

• Önce kesirlerin paydaları eşitlenir.
• Paydaları eşitlenmiş kesirlerin paylarının farkı sonucun payına yazılır.
• Paydaları eşitlenmiş kesirlerin ortak paydası sonucun paydasına aynen taşınır.
• Sonucun pay ve paydası ortak çarpan içeriyorsa sadeleştirme işlemi yapılır.
• Kesirlerden biri ya da ikisi tam sayılı kesir ise kesirler önce bileşik kesre çevrilerek çıkarma işlemi yapılabilir.

Kesirlerle Çarpma

İki ya da daha fazla kesir arasında çarpma işlemi aşağıdaki şekilde yapılır.

• Kesirlerin payları kendi aralarında çarpılır ve sonucun payına yazılır.
• Kesirlerin paydaları kendi aralarında çarpılır ve sonucun paydasına yazılır.

Çarpılan kesirlerin pay ve paydaları arasında çarpma işlemi öncesinde ya da sonrasında sadeleştirme yapılabilir.

Kesirlerle Bölme

Bir kesri diğer bir kesre bölmek için, ikinci (bölen) kesrin pay ve paydası aralarında yer değiştirir ve bölme işareti çarpma işaretine çevrilerek kesirler arasında çarpma işlemi yapılır.

Kesirlerden biri ya da ikisi tam sayılı kesir ise bu kesirler önce bileşik kesre çevrilir. İşlem sonucu bir bileşik kesir ise istenirse kesir tam sayılı kesre çevrilebilir.

Bölme işleminin terimlerinden biri tam sayı ise bu sayı paydası 1 olan bir kesir gibi düşünülerek bölme işlemine dahil edilir.

Kesirlerle bölme işlemi anlam olarak tam sayılarla bölme işlemi ile aynıdır ve bölüştürme/paylaştırma işlemine karşılık gelir.

Kesirlerde Üs Alma

Bir kesrin üssü alınırken, üs işlemi pay ve paydaya ayrı ayrı yansıtılır ve payın ve paydanın ayrı ayrı üssü alınır.

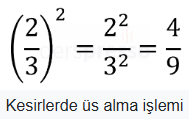
3.3. Kesir Problemleri Türleri

• Bütün-Parça İlişkisi: Bir bütünün belirli bir kısmının hesaplanması.
• Kesirlerle Oran-Orantı Problemleri: Oranlarla işlem yapılarak çözüm üretilir.
• Karışım ve Oran Problemlerinde Kesir Kullanımı: Kesirlerin farklı alanlardaki kullanım örnekleri.
• Kesirlerle Zamana Bağlı Problemler: Günlük hayat içerisinde saat hesaplamalarında kullanılan kesirler.
• Kesirlerde Denklem Kurma ve Çözme: Kesirli ifadelerle bilinmeyenleri içeren denklemleri çözme.

---

4. Sayı ve Kesir Problemlerinin Gerçek Hayatta Kullanıldığı Yerler

4.1. Finans ve Ekonomi

• Faiz hesaplamaları
• İndirim ve zam oranlarının hesaplanması
• Banka kredilerinde ödeme planlarının oluşturulması
• Vergi hesaplamaları

4.2. Yemek ve Mutfak

• Tariflerde malzeme ölçümleri (örneğin: 1/2 su bardağı şeker, 3/4 çay kaşığı tuz)
• Porsiyon hesaplamaları
• Besin değerlerinin hesaplanması
• Yemek maliyet analizleri

4.3. Zaman ve Ölçü Birimleri

• Saat ve dakikaların kesirli kullanımı (örneğin: 1,5 saat = 90 dakika)
• Uzunluk ölçümlerinde kesir kullanımı (örneğin: 3/4 metre kumaş)
• Harita ve ölçek hesaplamaları
• Navigasyon ve mesafe ölçümleri

4.4. Mühendislik ve Fizik

• İnşaat ve mimaride uzunluk hesaplamaları
• Malzeme oranları ve bölme işlemleri
• Elektrik devrelerinde direnç oranlarının hesaplanması
• Hidrolik sistemlerde basınç hesaplamaları
• Astronomi ve uzay bilimlerinde oran hesaplamaları

---

Sonuç:
Sayı ve kesir problemleri, hem sınavlarda hem de günlük hayatta karşılaşılan problemleri çözmek için büyük önem taşır. Bu konuları iyi kavrayarak, matematiksel düşünme becerinizi geliştirebilirsiniz. Ayrıca, finans, mühendislik, mutfak gibi birçok alanda kullanılan matematiksel hesaplamalar için temel oluşturur. Matematik, hayatın her alanında gereklidir ve sayı-kesir problemlerini anlamak, birçok pratik konuda başarı sağlamanıza yardımcı olabilir.

HAZIRLAYAN: ÇAĞATAY BEKİR AKIN 11/A 746