1.PERMÜTASYON

1.1 Permütasyonun özellikleri

2.TEKRARLI PERMÜTASYON

PERMÜTASYONUN GÜNLÜK HAYATTA KULLANIM ALANLARI

1. Bilgisayar Bilimleri ve Şifreleme

2. Genetik ve Biyoloji

3. Lojistik ve Ulaşım

4. Tiyatro ve Organizasyon

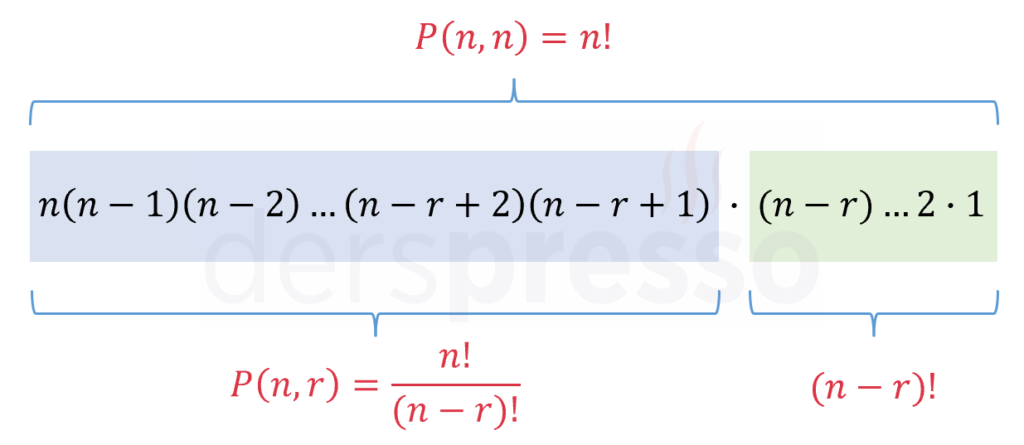
1.Permütasyon

n ve r birer doğal sayı ve r ≤ n olmak üzere n elemanlı bir kümenin birbirinden farklı r tane elemanından oluşan dizilişlerin her birine n’nin r’li permütasyonu (dizilişi) denir.

n ve r birer doğal sayı ve n r  olmak üzere,
n elemanlı bir kümenin r elemanlı her bir sıralanışına bu
kümenin r li permütasyonu denir.
n elemanlı bir kümenin tüm r li permütasyonlarının sayısı;
n! P(n, r)
(n r)!
dir.

Ya da kısaca,
r tan e
P(n, r) n (n 1) (n 2) (n r 1) yazılabilir.

7! 7! 7 6 5 4! P(7, 3)
(7 3)! 4!
  
 4!
 210
 P(5, 2) 5 4 20   
 P(6, 3) 6 5 4 120    
 P(n 3, 2) (n 3) (n 2)     
 n elemanlı bir kümenin tüm n li sıralanışlarının sayısı;
P(n, n) n!  dir.
 P(5, 5) 5! 120  

1.1. Permütasyonun özellikleri

n’nin sıfırlı permütasyonlarının sayısı

P (n, 0) = n!(n−0)!n!(n−0)! = n!n!n!n! = 1

ÖRNEK: P (8, 0) = 1

n’nin birli permütasyonlarının sayısı

P (n, 1) = n!(n−1)!n!(n−1)! = n.(n−1)!(n−1)!n.(n−1)!(n−1)! = n

ÖRNEK: P (8, 1) = 8

n’nin n’li permütasyonlarının sayısı

P (n, n) = n!(n−n)!n!(n−n)! = n!0!n!0! = n!

ÖRNEK: P (8, 8) = 8!

2.Tekrarlı permütasyon

n1
tanesi kendi aralarında özdeş, n2
tanesi kendi aralarında özdeş, …, nr
tanesi kendi aralarında özdeş olmak
üzere n n n n 1 2 r      tane nesnenin n li dizilişlerinin
her birine tekrarlı permütasyon denir.
Bu şekilde n tane nesnenin farklı dizilişlerinin sayısı;

1 2 r
n!
n ! n ! n !  
bağıntısı ile hesaplanır.