Mantığın Tanımı

Mantık, doğru düşünme kurallarını inceleyen ve akıl yürütme süreçlerini sistematik hale getiren bir disiplindir. 9. sınıf mantık konusu, önermeler, akıl yürütme türleri, çıkarım kuralları ve mantıksal ifadeler gibi temel kavramları içerir. Mantık, düşünceler arasındaki ilişkileri belirleyerek tutarlı ve geçerli sonuçlara ulaşmayı amaçlar. Matematik, felsefe, bilgisayar bilimi, hukuk gibi birçok alanda kullanılan mantık, bireylerin doğru kararlar almasına ve eleştirel düşünme becerilerini geliştirmesine yardımcı olur.

Mantık

• Önerme
• Bileşik Önerme
• Koşullu Önerme ve İki Yönlü Koşullu Önerme
• Her ve Bazı Niceleyicileri
• Tanım, Aksiyom, Teorem ve İspat Kavramları

Mantığın Günlük Hayatta Kullanıldığı Yerler

Mantık, birçok alanda kullanılan temel bir düşünme yöntemidir. Matematikte teoremleri ispatlarken, geometri ve cebir gibi konularda doğru çıkarımlar yapmak için mantık kurallarından yararlanılır.

Bilgisayar bilimlerinde algoritmaların oluşturulması, yapay zeka sistemlerinin geliştirilmesi ve programlamada mantıksal işlemler büyük önem taşır. Hukuk ve felsefe alanlarında akıl yürütme, tutarlı argümanlar oluşturma ve eleştirel düşünme süreçlerinde mantık kullanılır.

Fen bilimlerinde ise deney sonuçlarını analiz etme, hipotezleri test etme ve bilimsel çıkarımlar yapmada mantığın rolü büyüktür. Ayrıca, mühendislikte devre tasarımı ve sistem analizi gibi teknik alanlarda da mantık temel bir unsur olarak öne çıkar.

Günlük yaşamda ise doğru kararlar almak, olayları mantıklı bir şekilde değerlendirmek ve problemleri çözmek için mantıklı düşünme becerileri gereklidir. Bu nedenle mantık, hem akademik hem de günlük hayatta önemli bir yere sahiptir.

Önerme Nedir?

Önerme, doğru ya da yanlış olduğu kesin bir şekilde belirlenebilen bir ifadedir. Diğer bir deyişle, bir önermenin doğruluğu kanıtlanabilir. Ancak bir soru, emir ya da dilek cümlesi önerme olamaz, çünkü bu tür ifadelerin doğruluğu ya da yanlışlığı tartışmaya açıktır.

Önerme örnekleri:

• Doğru bir önerme: “5+5=10’dur.”
• Yanlış bir önerme: “Konya bir şehir değildir.”
• Önerme olmayan bir ifade: “Bugün dışarı çıkmalısın.”

Mantığın Temel Kavramları

Önermeler ve Önermenin Doğruluk Değeri

Bir ifadenin doğru ya da yanlış olabilmesi için kesin bir yargı bildirmesi gerekir. Bu tür ifadelere önermeler denir.

• Örnek Önermeler:
  • “Ankara Türkiye’nin başkentidir.” (Doğru)
  • “3 bir asal sayıdır.” (Yanlış)
  • “İstanbul bir şehir değildir.” (Yanlış)

Ancak “Keşke hava güzel olsaydı.” gibi ifadeler bir yargı bildirmediği için önerme değildir.

Birleşik Önermeler

1) “Ve” Bağlacı:

İki veya daha fazla önermenin “ve”, “veya”, “ya da”, “ise”, “ancak ve ancak” gibi bağlaçlarla birbirine bağlanmasıyla elde edilen yeni önermeye bileşik önerme denir. “ve” Bağlacı: “∧” sembolü ile gösterilir.

Örnekler:

• p: Güneş Parlıyor. (Doğru)
• q: Köpekler havlar.(Doğru)
• p ∧ q: Güneş parlıyor ve köpekler havlar.

Doğruluk Tablosu

Burada “p ∧ q” ifadesi yalnızca her iki önerme de doğru olduğunda “doğru” olur.

2) “Veya” Bağlacı:

“veya” Bağlacı: “∨” sembolü ile gösterilir. Buna dikkat: p ile q önermelerinden en az biri doğru iken p ∨ q bileşik önermesinin doğruluk değeri 1, her ikisi de yanlış iken doğruluk değeri 0’dır.

Örnekler:

p ∨ q: Ay Dünya’nın etrafında döner veya filler uçabilir. D ∨ Y = D

p ∨ q: Ay Dünya’nın etrafında döner veya filler yürür. D ∨ D =D

Doğruluk Tablosu

3) “Ya da” Bağlacı:

“ya da” Bağlacı: “⊻” sembolü ile gösterilir. Buna dikkat: “⊻” bağlacında önermelerin doğruluk değeri aynı ise sonuç 0, farklı ise sonuç 1’dir.

Örnekler:

p ⊻ q: 1 km 1000 m’dir YA DA 1 kg 1000 gr’dır. (Yanlış)

p ⊻ q: EBOB(12, 18) = 3 YA DA EKOK(12, 18) = 36 (Doğru)

p ⊻ q: Bir noktadan geçen tek bir doğru çizilebilir YA DA Paralel iki doğru tek bir noktada kesişirler. (Yanlış)

Doğruluk Tablosu

4) Koşullu Önerme ve İki Yönlü Koşullu Önerme

Koşullu Önerme (“ise” Bağlacı)

Bir p ve q önermesi için “p ⇾ q” ifadesi, “Eğer p doğruysa, o zaman q da doğrudur.” anlamına gelir.

• p: Ön koşul
• q: Sonuç
• “p ⇾ q” p olduğunda q’nun da olması gerektiğini ifade eder.

Örnekler:

• p: Hava yağmurlu (Doğru)
• q: Şemsiyemi yanıma alırım (Doğru)
• p ⇾ q: “Eğer hava yağmurluysa, şemsiyemi yanıma alırım.”

Doğruluk Tablosu

Koşullu önermenin yanlış olduğu tek durum, öncül (p) doğru olduğu halde sonuç (q) yanlışsa oluşur.

• Örnekler:

• “Eğer Ahmet çalışırsa (p), sınavı geçer (q).”
  • Ahmet çalıştı ve sınavı geçti → (Doğru)
  • Ahmet çalıştı ama sınavdan kaldı → (Yanlış)
  • Ahmet çalışmadı ama sınavı geçti → (Doğru)
  • Ahmet çalışmadı ve sınavdan kaldı → (Doğru)

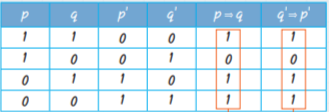
Koşullu Önermenin Karşıtı, Tersi ve Karşıt Tersi

p⇒ q önermesinin karşıtı q⇒ p
p⇒ q önermesinin tersi p’⇒ q’
p⇒ q önermesinin karşıt tersi q’⇒ p’ olur.
p⇒ q önermesi karşıt tersi olan q’⇒ p’
önermesine denktir.

Doğruluk Tablosu

5) İki Yönlü Koşullu Önerme (↔) (Ancak ve ancak…)

“p ⇿ q” ifadesi, “p ancak ve ancak q ise doğrudur.” anlamına gelir. Yani hem p hem q aynı doğruluk değerine sahip olmalıdır.

• Örnekler:

p ⇿ q: “Bir sayı ancak ve ancak 4’e tam bölünüyorsa çifttir.”

p: Bir sayı 4’e tam bölünür.

q: Sayı çifttir.

Doğruluk Tablosu

İki yönlü koşullu önermenin doğru olması için, iki önerme de aynı doğruluk değerine sahip olmalıdır.

• Örnekler:

• “Bir üçgen eşkenar ise, ancak ve ancak iç açılarının hepsi 60°’dir.”
  • Üçgen eşkenar ve açıları 60° ise → (Doğru)
  • Üçgen eşkenar ama açıları 60° değilse → (Yanlış)

Her ve Bazı Niceleyicileri

∀ sembolü “her” anlamına gelir. Bütün, tamamı sözcükleri ile aynı anlamda kullanılır.
Evrensel niceleyici olarak tanımlanır. ∃ sembolü “bazı” anlamına gelir. En az bir ifadesi ile aynı anlama gelir. Varlıksal niceleyici olarak tanımlanır.

Tanım, Aksiyom, Teorem ve İspat Kavramları

Her bilim dalının kendine özgü anlamlar içeren sözcükleri ve dili vardır. Bu özel anlam içeren ifadelerin her birine terim denir. Anlamları daha önceden bilinen terimler yardımıyla bir terimin özelliklerini belirtmeye veya ifade etmeye tanım denir.
Doğruluğu ispatsız kabul edilen önermelere aksiyom denir. p ve q önermeler olmak üzere p önermesi doğru iken p⇒ q önermesinin doğruluğu ispatlanabiliyorsa p⇒ q önermesine teorem denir. p⇒ q teorem olmak üzere p önermesine hipotez, q önermesine hüküm denir. Bir teoremin hipotezi doğru olduğunda hükmünün
de doğru olacağını gösteren işlemler bütününe ispat denir.