ÜÇGENDE AÇILAR

1.ÜÇGEN NEDİR

2.ÜÇGENİN TEMEL ELEMANLARI

3.ÜÇGENİN AÇI ÖZELLİKLERİ

4.AÇILARINA GÖRE ÜÇGENLER

a) Dar Açılı Üçgen

b) Dik Açılı Üçgen

c) Geniş Açılı Üçgen

5.KENARLARINA GÖRE ÜÇGENLER

a) Çeşitkenar Üçgen

b) İkizkenar Üçgen

c) Eşkenar Üçgen

6.ÜÇGENİN YARDIMCI ELEMANLARI

a) Kenarortay

b) Açıortay

b.1) İç Açıortay Teoremi

b.2) Dış Açıortay Teoremi

b.3) Dış Teğet Çember

7. ÜÇGENDE AÇILARIN KULLANIM ALANLARI

8. ÜÇGENDE AÇILAR İLE İLGİLİ SORULAR

1) ÜÇGEN NEDİR ? Aynı doğru üzerinde olmayan üç noktanın birleşmesi ile oluşan çokgene üçgen denir.

ÖRNEK: [AB] ∪∪ [BC] ∪∪ [AC] = ABC üçgeni

2) ÜÇGENİN TEMEL ELEMANLARI

Üçgenin temel elemanları köşeleri, kenarları ve açılarıdır.

• A, B, C noktaları üçgenin köşeleridir.
• [AB], [BC] ve [AC] üçgenin kenarlarıdır.
• a, b, c üçgenin iç açılarıdır.
• x, y, z üçgenin dış açılarıdır.

3) ÜÇGENİN AÇI ÖZELLİKLERİ

Bir üçgenin iç açılarının ölçüleri toplamı 180°dir.

ÖRNEK:

x + y + z =  180°dir.

İSPATI:

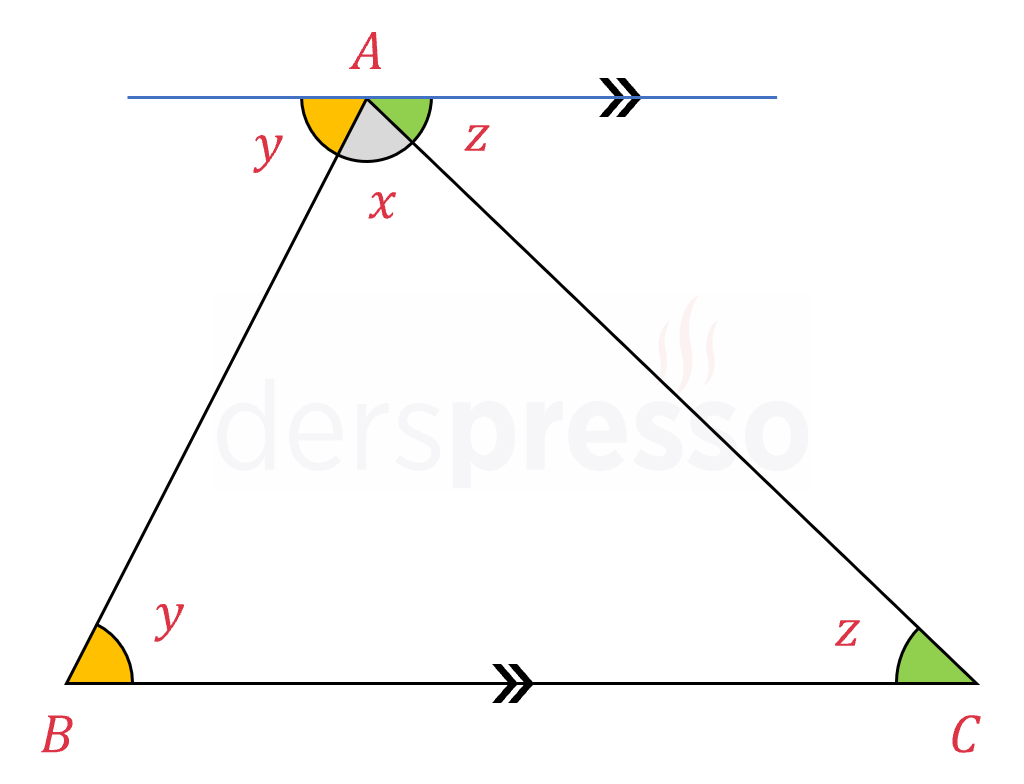
1. A köşesinden geçen ve a kenarına paralel bir doğru çizelim.
2. Z kuralına göre Â iç açısına komşu iki açı, üçgenin taban iç açıları ile iç ters açılardır.
3. Dolayısıyla x, y ve z açıları bütünler açılardır ve toplamları 180° olur.

Bir üçgenin dış açılarının ölçülerinin toplamı ise 360°dir.

ÖRNEK:

x’ + y’ + z’ =  360°dir.

İSPATI:

1. Üçgenin iç açıları toplamı 180°’dir.
2. x + y + z = 180°dir.
3. Üçgenin dış açılarını iç açılar cinsinden yazalım.
4. x′=180°− x, y′=180°− y,  z′=180°− z
5. x ′+ y′ + z’ = (180°−x) + (180°−y) + (180°−z)
6. x′ + y′ + z′ = 540 °− (x + y + z) 

Bir dış açının ölçüsü, kendisine komşu olmayan iki iç açının toplamına eşittir.

x’= y + z y’= x + z z’= x + y

İSPATI:

İspat 1:

A noktasından geçen ve [BC] kenarına paralel bir doğru çizelim (mavi doğru).

Bu doğru parçası x′ açısını iki farklı açıya ayırır ve oluşan açılar y açısının yöndeş açısı ve z açısının iç ters açısı olur.

Buna göre x′ açısını bu iki açının toplamı şeklinde aşağıdaki şekilde yazabiliriz.

x’= y + z

İspat 2:

Üçgenin iç açıları toplamı 180°’dir.

x + y + z = 180°

x= 180° − (y + z)

Bir dış açıyı iç açı cinsinden yazalım.

x′= 180° − x

Bu denklemde x yerine bir önceki denklemdeki eşitini yazalım.

x’= 180° − (180° − (y + z)) = y + z

4. AÇILARINA GÖRE ÜÇGENLER

a) Dar Açılı Üçgen

Dar açı, 90°’den küçük olan açılara denir.

Dar açılı üçgen ise, tüm açıları dar açı olan üçgenlere denir.

b) Dik Açılı Üçgen

Dik açı, 90° olan açılara denir.

Dik açılı üçgen ise, bir açısı dik açı olan diğer iki açısı dar açı olan üçgenlere denir.

c) Geniş Açılı Üçgen

Geniş açı, 90°’den büyük olan açılara denir.

Geniş açılı üçgen ise, bir açısı geniş açı diğer iki açısı dar açı olan üçgenlerdir.

5. KENARLARINA GÖRE ÜÇGENLER

a) Çeşitkenar Üçgen

Tüm kenar uzunlukları birbirinden farklı olan üçgenlere denir.

Çeşitkenar üçgenin açılarının ölçüleri de birbirinden farklıdır.

b) İkizkenar Üçgen

İki kenar uzunluğu eşit olan üçgenlere denir.

İkizkenar üçgende eşit uzunluktaki kenarların birleştiği köşedeki açıya (A) tepe açısı, diğer iki açıya (B ve C) taban açıları denir. Taban açılarının ölçüleri birbirine eşittir.

c) Eşkenar Üçgen

Tüm kenar uzunlukları eşit olan üçgenlere denir.

Eşkenar üçgende tüm açıların ölçüleri birbirine eşittir ve 60°’dir.

6. ÜÇGENİN YARDIMCI ELEMANLARI

a) Kenarortay

Üçgenin bir köşesini karşı kenarın orta noktasına birleştiren doğru parçasına üçgenin o kenarına ait kenarortayı denir.

A, B ve C köşelerine ait kenarortaylar sırasıyla V_a, V_b ve V_c ile gösterilir. Üçgenin üç kenarortayı üçgenin içinde bir noktada kesişir ve bu noktaya üçgensel bölgenin ağırlık merkezi denir.

NOT:

Bir dik üçgende hipotenüse ait kenarortayın uzunluğu hipotenüsün yarısına eşittir.

b) Açıortay

Üçgenin bir iç açısını iki eş parçaya bölen ve karşı kenarı kesen doğru parçasına açıortay ya da iç açıortay denir.

 A, B ve C köşelerine ait açıortaylar sırasıyla n_a, n_b ve n_c ile gösterilir.

Bir üçgenin iç açıortayları her zaman tek bir noktada ve üçgenin içinde kesişir. İki açıortayın kesiştiği nokta biliniyorsa üçüncü açıortay da bu noktadan geçmek zorundadır. Bu nokta aynı zamanda üçgenin r yarıçaplı iç teğet çemberinin merkezidir.

Bir açıortayın herhangi bir noktasından açıortayın kollarına indirilen dikmelerin uzunlukları birbirine eşittir. Aynı zamanda bu dikmelerin açıortayın kollarını kestiği noktalardan açıortayın köşesine olan uzunluklar da eşittir.

[AN], A köşesine ait iç açıortay,

[DN]⊥[AB] ve [NE]⊥[AC] olmak üzere,

[DN]=[EN]

[AD]=[AE]

İSPATI:

Açıortay üzerindeki bir C noktasından açının kollarına indirilen dikmelerin ve açının kolları üzerinde oluşan doğru parçalarının uzunluklarının eşit olduğunu ve oluşan iki üçgenin eş üçgenler olduğunu gösterelim.

m(AOC^)=m(EOC^)

m(OAC^)=m(OEC^)=90°

AOC ve EOC üçgenlerinin ikişer açısı eşit olduğu için, üçüncü açıları da eşittir, dolayısıyla iki üçgen benzerdir.

[OC] kenarı bu iki üçgen için ortak kenar olduğu için, üçgenlerin benzerlik oranı 1’dir, dolayısıyla bu iki üçgen aynı zamanda eş üçgenlerdir. Buna göre, aşağıdaki kenar uzunlukları da eşittir.

|CA|=|CE|

|OA|=|OE|

Bir üçgenin en uzun açıortayı üçgenin en kısa kenarına aittir.

a ≥ b ≥ c ise,

n_a küçük eşittir n_b‘den, n_b ise küçük eşittir n_c‘den

Bir üçgenin iç teğet çemberinin merkezi ile üçgenin köşelerini birleştiren doğru parçalarının oluşturduğu alanlar, her alanın komşu olduğu kenar uzunluğu ile doğru orantılıdır.

I üçgenin iç teğet çemberinin merkezi olmak üzere,

A(BIC) / a = A(CIA) / b = A(AIB) / c = k

İSPATI:

İç teğet çemberin merkezi olan I noktasından üçgenin kenarlarına birer dikme çizelim.

Bu dikmeler aynı zamanda iç teğet çemberin birer yarıçapıdır.

İç teğet çemberin yarıçapı ABC üçgeninin kenarlarına teğet olduğu için yarıçap üç kenarı da dik keser, dolayısıyla aynı zamanda üç üçgenin de yüksekliğidir.

Buna göre üçgenlerin alanlarını aşağıdaki gibi yazabiliriz.

A(ABI)=c⋅r / 2

A(BCI)=a⋅r / 2

A(CAI)=b⋅r / 2

Her eşitlikte kenar uzunluklarını eşitliğin sol tarafına aldığımızda ilgili alanların kenar uzunluklarına oranının sabit olduğunu görürüz.

A(ABI) / c = r / 2

A(BCI) / a = r / 2

A(CAI) / b = r / 2

A(BIC) / a = A(CIA) / b = A(AIB) / c = r / 2 = k

b.1) İç Açıortay Teoremi

Üçgenin bir köşesinden karşı kenara çizilen iç açıortayın iki yanındaki kenarların uzunluk oranı, açıortayın karşı kenarda böldüğü parçaların uzunluk oranına eşittir. Yükseklikleri aynı iki üçgenin alanlarının oranı taban uzunlukları ile orantılı olduğu için, bu orantıya açıortayın ayırdığı iki üçgenin alanlarının oranını da ekleyebiliriz.

[AN], A köşesine ait iç açıortay olmak üzere,

c / b = m / n = A(ABN) / A(ANC)

b.2) Dış Açıortay Teoremi

Üçgenin bir köşesinden çizilen dış açıortay için aşağıdaki orantı geçerlidir.

[AN], A köşesine ait bir dış açıortay olmak üzere,

c / b = m / n

Bir köşeden çizilen iç ve dış açıortaylar bütünler iki açıyı iki eşit açıya böldükleri için iç ve dış açıortayların arasında oluşan açı 90° olur.

x + y = 90° 

b.3) Dış Teğet Çember

Bir üçgenin iki dış açıortayı ile bir iç açıortayı üçgenin dışında bir noktada kesişir. Bu nokta üçgenin dış teğet çemberlerinden birinin merkezidir. Dış teğet çember üçgenin bir kenarına ve diğer iki kenarın üçgenin dışındaki uzantılarına teğettir.

Bir üçgenin her biri bir kenara dıştan teğet olmak üzere toplam üç farklı dış teğet çemberi vardır.

7. ÜÇGENDE AÇILARIN KULLANIM ALANLARI

Üçgen ve açıları günlük hayatımızda birçok yerde kullanıyoruz.

Örneğin,

Üçgende açılar, harita okuma, rota planlama ve GPS kullanımında yön tayininde yardımcı olur. Mesela, bir aracın hangi yöne döneceğini belirlemek için açıları kullanabilirsiniz.

Evlerin, binaların ve diğer yapıların tasarımı ve inşası sırasında açılar önemlidir. Duvarların, tavanların ve zeminlerin yerleşimi, açıların hesaplanmasına dayanır.

8. ÜÇGENDE AÇILAR İLE İLGİLİ SORULAR