1. Kullanım Alanları
2 . Genel Alan Bağıntısı
3. Dik Üçgende Alan
4. Geniş Açılı Üçgende Alan
5. Bir Açısı Ve Bu Açının Kenarları Bilinen Üçgenin Alanı
6.Üç Kenarının Uzunluğu Verilen Üçgenin Alanı
7. Çevresi Ve İç Teğet Çemberinin Yarıçapı Verilen Üçgenin Alanı
ÜÇGENDE ALAN
Aynı doğru üzerinde olmayan üç noktanın birleşmesi ile oluşan çokgene üçgen denir. Üçgenin 3 köşesi, 3 kenarı ve 3 açısı vardır.

İskenderiyeli HERON ,Matematikte çoğunlukla, bir üçgenin alanını yalnızca kenarlarının uzunluklarını kullanarak hesaplamanın bir yolu olan Heron formülü ile hatırlanır. Babil ve Mısır geometrilerini Yunan geometri biçimiyle birleştirip, yalnızca uygulamada işe yarayan formülleri kitaplarında kullanmıştır
Osmanlı döneminde de üçgene müselles, alana Mesaha-i sathiye, dik açıya zaviye-i kaime, yüksekliğe kaide irtifaı deniliyordu. Üçgenin alanını için “Üçgenin alanı taban uzunluğu ile yüksekliğinin çarpımının yarısına eşittir” tanımı yerine, “Bir müsellesin mesaha-i sathiyyesi kaidesinin irtifasına hâsıl-ı zarbinin nısfına müsavidir” tanımı kullanılıyordu.
1. KULLANIM ALANLARI NELERDİR ?

Üçgenler, geometride ve günlük hayatta birçok alanda kullanılır. Örneğin, binalar, köprüler, gemiler ve uçaklar gibi yapılarda üçgenler kullanılır. Çünkü üçgenler, dayanıklı ve sağlam yapılardır.
Binalar: Binaların temelleri, çatıları ve destekleyici kolonları genellikle üçgen şeklindedir. Bu, binalara daha fazla sağlamlık ve dayanıklılık sağlar.
Köprüler: Köprüler, genellikle üçgen şeklindeki kirişlerin üzerine inşa edilir. Bu, köprülere daha fazla sağlamlık ve dayanıklılık sağlar.
Gemiler: Gemilerin gövdeleri, genellikle üçgen şeklindeki direklerle desteklenir. Bu, gemilere daha fazla sağlamlık ve dayanıklılık sağlar.
Uçaklar: Uçakların kanat ve kuyrukları genellikle üçgen şeklindedir. Bu, uçaklara daha fazla kaldırma kuvveti ve kararlılık sağlar.
Üçgenler ve Seyahat: Trafik işaretlerinde, özellikle uyarı ve dur işaretlerinde üçgen şekilleri kullanılır. Bu, sürücülere önemli bilgiler iletmek için etkili bir yöntemdir.



2. GENEL ALAN BAĞINTISI
Bir üçgenin alanı, bir kenarı ile o kenara ait yüksekliğin çarpımının yarısıdır.
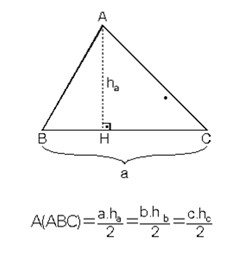
Hangi kenarı kullanırsak kullanalım üçgenin alanı sabittir.
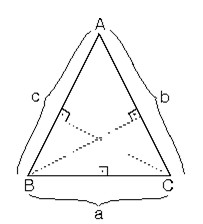
Bir ABC üçgeninde yükseklik her zaman üçgenin içinde olmayabilir.
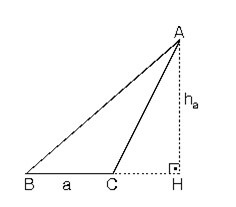
ÖRNEK SORU ÇÖZELİM
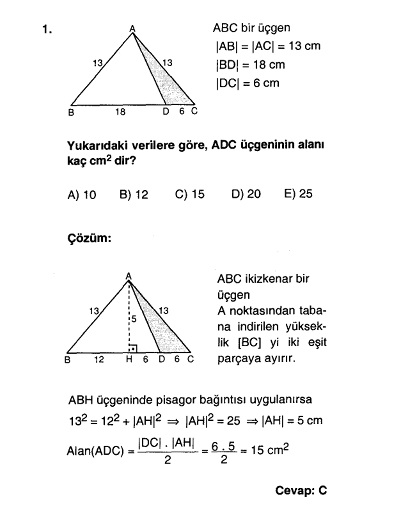
3. DİK ÜÇGENDE ALAN
Dik Üçgen, iç açılarından bir tanesinin ölçüsü 90 derece olan üçgendir.
b dik açının komşu kenarlarından bir tanesi, c ise komşu kenarlardan ikincisinin uzunluğu olmak üzere;
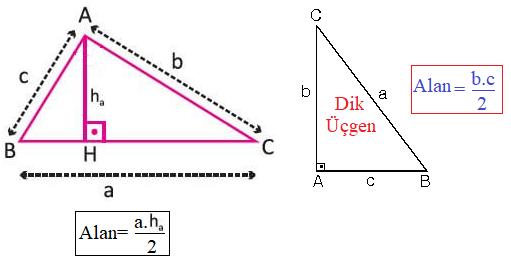
Alan = b × c / 2 formülüyle hesaplanır. Bir dik üçgen, dikdörtgenin köşeden köşeye kesilmiş halidir. Dikdörtgenin alanını hesaplarken kenar uzunluklarını çarparız. Bu durumda bu uzunluğu 2’ye bölersek dik üçgenin alanını buluruz.
ÖRNEK SORU ÇÖZELİM
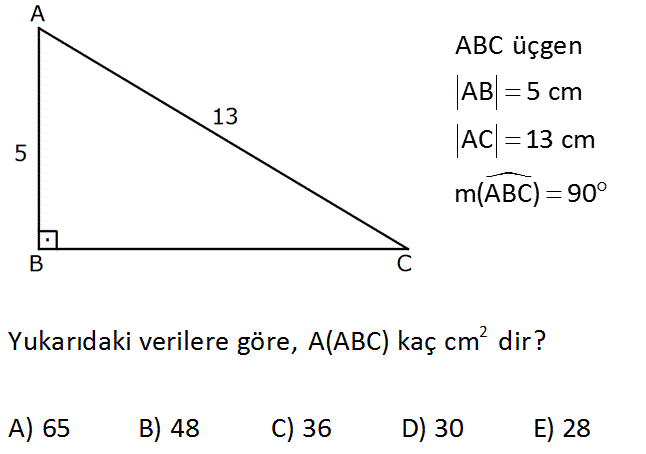

4. GENİŞ AÇILI ÜÇGENDE ALAN
Geniş açılı üçgenlerde [AB] ve[BC] kenarlarına ait yükseklikler üçgenin dış bölgesindedir.
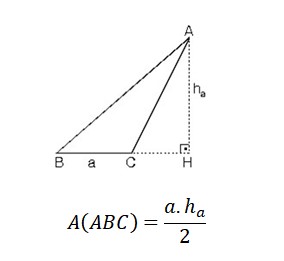
ÖRNEK SORU ÇÖZELİM

Şekilde verilen ABC üçgenin alanı kaç cm2 dir?
CÖZÜM : 12 cm lik kenara ait yükseklik 7 cm lik AH uzunluğudur.

5. BİR AÇISI VE BU AÇININ KENARLARI BİLİNEN ÜÇGENİN ALANI
ABC üçgeninde m(ABC) = a |AB| = c|BC| = a
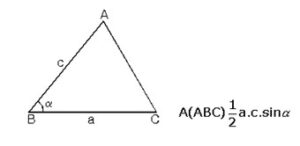
Birbirini 180° ye tamamlayan açıların sinüsleri eşit olduğundan;
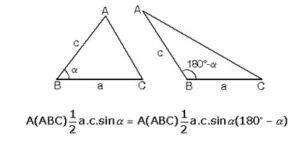
|BC| = a |AB| = c uzunlukları sabit olan ABC üçgeninin alanının maksimum olabilmesi için a = 90° olmalıdır.
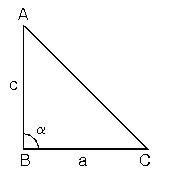
Hipotenüs uzunluğu sabit olan ABC dik üçgeninin alanının en büyük değerini alabilmesi için |AB| = |AC| olmalıdır.ABC üçgeni ikizkenar dik üçgen olmalıdır.
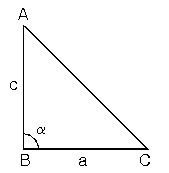
6. ÜÇ KENARI VERİLEN ÜÇGENİN ALANI
3 kenarının uzunluğu bilinen ancak aradaki herhangi bir açının bilinmediği üçgenlerde de alan bulunabilir. Burada u alan formülü olarak da bilinen üçgenin çevresinden hareketle alan bulunmaktadır.
Üçgenin 3 kenar uzunluğuna sırasıyla A, B ve C olursa çevresi de A + B + C ile bulunur. Burada A + B + C = 2U dersek U çevrenin yarısı olacaktır.
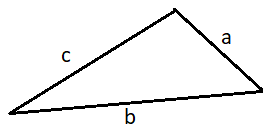
Burada ALAN = √(U(U -A) (U – B) (U – C)) formülü kullanılabilir.
ÖRNEK OLARAK ;
kenar uzunlukları 6, 8 ve 10 alan bir üçgenin alanını bulmak için önce çevre uzunluğunu buluruz. Çevre 6 + 8 + 10 = 24’tür. 24’ün yarısı alınır. Yani u = 12 olur. Formülü uygularsak √(12(12 – 6)(12 – 8)(12 – 10)) = √(12.6.4.2) = √576 = 24 bulunur.
7. ÇEVRESİ VE İÇ TEĞET ÇEMBERİNİN YARIÇAPI VERİLEN ÜÇGENİN ALANI
Herhangi bir ABC üçgeninin kenarlarına sırasıyla a, b, c uzunluklarını verelim. Bu üçgenin iç teğet çemberinin yarıçapına da r diyelim.
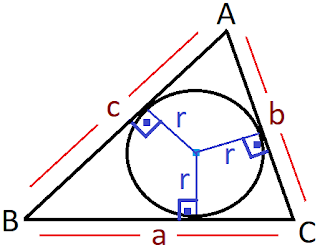
Çemberin merkezinden üçgenin kenarlarına doğrular çektiğimizde ABC üçgenini üç alana ayırmış oluruz.
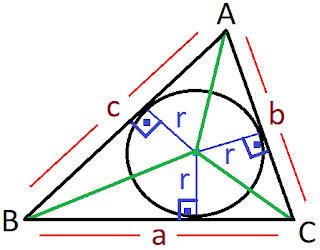
Her bir üçgenin alanını üçgenin klasik alan formülünden hesaplayabiliriz. Üç alanın toplamı Alan(ABC)’yi verir. [Buradaki alan formülünde (a+b+c) / 2 yerine u dedik.]


Bir yanıt yazın